
����Ŀ�������߳��ֱ�Ϊ![]() ����������ͼ�ٷ��ã���δ�غϲ���(��Ӱ����)���ΪS1 �� ��ͼ���д������ε����½ǰڷ�һ���߳�Ϊb��С�����Σ��õ�ͼ�ڣ������߳�Ϊb��С�������غϲ���(��Ӱ����)���ΪS2.
����������ͼ�ٷ��ã���δ�غϲ���(��Ӱ����)���ΪS1 �� ��ͼ���д������ε����½ǰڷ�һ���߳�Ϊb��С�����Σ��õ�ͼ�ڣ������߳�Ϊb��С�������غϲ���(��Ӱ����)���ΪS2.
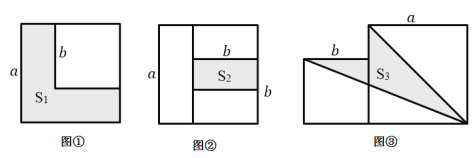
��1���ú�a��b�Ĵ���ʽ�ֱ��ʾS1��S2.
��2����a+b=9��ab=21����S1+S2��ֵ.
��3���������߳��ֱ�Ϊa��b����������ͼ�۷��ã���S1+S2=30ʱ�����ͼ������Ӱ���ֵ����S3.
���𰸡�(1) S1=a2-b2,S2=2b2-ab;(2)18;(3)15;
��������
��1����ͼ�������κͳ����ε������ϵ���ɵô𰸣�
��2������S2+S2=a2-b2+2b2-ab=a2+b2-ab����a+b=9��ab=21������м��㼴�ɣ�
��3������S3=a2+b2-![]() b��a+b��-
b��a+b��-![]() a2=
a2=![]() ��a2+b2-ab����S2+S2=a2+b2-ab=30�������ͼ3����Ӱ���ֵ����S3��
��a2+b2-ab����S2+S2=a2+b2-ab=30�������ͼ3����Ӱ���ֵ����S3��
��1����ͼ�١�ͼ�ڣ���S1=a2-b2��S2=2b2-ab��
��2����a+b=9��ab=21
��S1+S2=a2-b2+2b2-ab=a2+b2-ab=(a+b)2-3ab=81-3��21=18��
��S1+S2��ֵΪ18��
��3����ͼ�ۣ���S3=a2+b2-![]() b(a+b)-
b(a+b)-![]() a2=
a2=![]() (a2+b2-ab)��
(a2+b2-ab)��
��S1+S2=a2+b2-ab=30��
��S3=![]() ��30=15��
��30=15��
��ͼ������Ӱ���ֵ����S3Ϊ15


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() ��
��![]() �ύ��
�ύ��![]() ��
��![]() ���㣬��
���㣬��![]() �ύ��
�ύ��![]() �㣬��
�㣬��![]() ��
��

��1���������ߵĽ���ʽ������![]() �����ꣻ
�����ꣻ
��2���ж�![]() ����״��֤����Ľ��ۣ�
����״��֤����Ľ��ۣ�
��3����![]() ��
��![]() ���ϵ�һ�����㣬��
���ϵ�һ�����㣬��![]() ��ֵ��Сʱ����
��ֵ��Сʱ����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����5��5�������������У����ڸ���ϵĵ�A��B��C��D����ȡ���㣬�����ɵ�������ǡ����ֱ�������εĸ���Ϊ��������

A. 1 B. 2 C. 3 D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�Ҿ��̳��ƻ�����ij�ֲ��������ν������ۣ��й���Ϣ���±���
ԭ���ۣ�Ԫ/�ţ� | ���ۼۣ�Ԫ/�ţ� | �����ۼۣ�Ԫ/�ף� | |
���� | a | 270 | 500 |
���� | b | 70 |
������3�Ų���18�Ų�����Ҫ1170Ԫ��������5�Ų���25�Ų�����Ҫ1750Ԫ��
��1�������a��b��ֵ��
��2�������̳��������ε������Dz���������5������20�ţ��Ҳ����Ͳ��ε�������������200�ţ����̳��ƻ���ȫ�������������ۣ�һ�Ų��������Ų������һ�ף���������������۷�ʽ���ۣ��蹺������������Ϊx���ţ���������ΪW��Ԫ������W����x�ĺ�����ϵʽ����������������ʱ�Ľ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������OABC�У���A�������ǣ���3��1������B����������4����B��C���������ֱ��ǣ�������
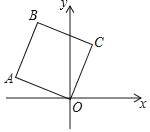
A. ����2��4������1��3�� B. ����2��4������2��3��
C. ����3��4������1��4�� D. ����3��4������1��3��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����š�������+��ʱ���ĵ�����һ�����ʹ�ʽ�ܵ����ڻ�ӭ���ô�ʽ���ܷ�������̷Ѻͺ�ʱ����ɣ�������̷Ѱ�xԪ/������㣬��ʱ�Ѱ�yԪ/���Ӽ��㣨�ܷ��ò���9Ԫ��9Ԫ�Ƽۣ���С����С�������øô�ʽ���У��������Ƽ۹�������ܷ��á���ʻ��������ʱ�������
ʱ�䣨���ӣ� | ���������� | ���ѣ�Ԫ�� | |
�� | 8 | 8 | 12 |
�� | 12 | 10 | 16 |
��1����x��y��ֵ��
��2�����С��Ҳ�øô�ʽ������ʻ��11�������14���ӣ���ôС���Ĵ��ܷ���Ϊ���٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������OABC�����������������ϣ�����������y=![]() ��ͼ���ڵ�һ���ķ�֧��AB���е�D��OB�ڵ�E������EC������OEC�����Ϊ12����k=_____��
��ͼ���ڵ�һ���ķ�֧��AB���е�D��OB�ڵ�E������EC������OEC�����Ϊ12����k=_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪Rt��ABC�У���BAC=90��������ABC�Ƶ�A˳ʱ����ת��ʹ��D��������CA�ϣ�DE���ӳ��߽�BC��F������CFD�Ķ���Ϊ��������

A. 80�� B. 90�� C. 100�� D. 120��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com