
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,且
点,且![]() .
.

(1)求抛物线的解析式及顶点![]() 的坐标;
的坐标;
(2)判断![]() 的形状,证明你的结论;
的形状,证明你的结论;
(3)点![]() 是
是![]() 轴上的一个动点,当
轴上的一个动点,当![]() 的值最小时,求
的值最小时,求![]() 的值.
的值.
【答案】(1)y=![]() x2-
x2-![]() x-2,顶点D的坐标为(
x-2,顶点D的坐标为(![]() ,-
,-![]() );(2)△ABC是直角三角形,理由见解析;(3)m=
);(2)△ABC是直角三角形,理由见解析;(3)m=![]() .
.
【解析】
试题分析:(1)把点A代入函数解析式即可求得b值,可得抛物线的解析式,根据解析式直接求得顶点D的坐标即可;(2)由函数解析式可以求得其与x轴、y轴的交点坐标,即可求得AB、BC、AC的长,由勾股定理的逆定理可得三角形的形状;(3)先求得C关于x轴的对称点C′,求得直线C′D的解析式,与x轴的交点的横坐标即是m的值.
试题解析:(1)∵点A(-1,0)在抛物线y=
![]() x2+bx-2上,
x2+bx-2上,
∴![]() ×(-1)2+b×(-1)-2=0,
×(-1)2+b×(-1)-2=0,
解得,b=-![]()
∴抛物线的解析式为y=![]() x2-
x2-![]() x-2
x-2
y=![]() x2-
x2-![]() x-2=
x-2=![]() (x2-3x-4)=
(x2-3x-4)=![]() (x-
(x-![]() )2-
)2-![]() ,
,
∴顶点D的坐标为(![]() ,-
,-![]() ).
).
(2)当x=0时y=-2,
∴C(0,-2),OC=2.
当y=0时,
![]() x2-
x2-![]() x-2=0,
x-2=0,
∴x1=-1,x2=4,
∴B(4,0).
∴OA=1,OB=4,AB=5.
∵AB2=25,AC2=OA2+OC2=5,BC2=OC2+OB2=20,
∴AC2+BC2=AB2.
∴△ABC是直角三角形.
作出点C关于x轴的对称点C′,则C′(0,2),OC′=2,连接C′D交x轴于点M,根据轴对称性及两点之间线段最短可知,MC+MD的值最小.
设直线C′D的解析式为y=kx+n,
则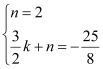 ,
,
解得n=2,k=-![]() .
.
∴y=-![]() x+2.
x+2.
∴当y=0时,-![]() x+2=0,x=
x+2=0,x=![]() .
.
∴m=![]() .
.


科目:初中数学 来源: 题型:
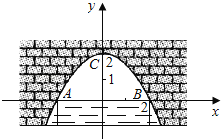
【题目】图中是抛物线形拱桥,当拱顶离水面2m时,水面宽4m,建立如图所示的平面直角坐标系:
(1)求拱桥所在抛物线的解析式;
(2)当水面下降1m时,则水面的宽度为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l1:y=﹣![]() x与反比例函数y=
x与反比例函数y=![]() 的图象交于A,B两点(点A在点B左侧),已知A点的纵坐标是2:
的图象交于A,B两点(点A在点B左侧),已知A点的纵坐标是2:
(1)求反比例函数的表达式;
(2)将直线l1:y=﹣![]() x向上平移后的直线l2与反比例函数y=
x向上平移后的直线l2与反比例函数y=![]() 在第二象限内交于点C,如果△ABC的面积为30,求平移后的直线l2的函数表达式.
在第二象限内交于点C,如果△ABC的面积为30,求平移后的直线l2的函数表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:AB为⊙O的直径,C是⊙O上一点,如图,AB=12,BC=4![]() .BH与⊙O相切于点B,过点C作BH的平行线交AB于点E.
.BH与⊙O相切于点B,过点C作BH的平行线交AB于点E.
(1)求CE的长;
(2)延长CE到F,使EF=![]() ,连接BF并延长BF交⊙O于点G,求BG的长;
,连接BF并延长BF交⊙O于点G,求BG的长;
(3)在(2)的条件下,连接GC并延长GC交BH于点D,求证:BD=BG.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一种实验用轨道弹珠,在轨道上行驶5分钟后离开轨道,前2分钟其速度v(米/分)与时间t(分)满足二次函数v=at2,后三分钟其速度v(米/分)与时间t(分)满足反比例函数关系,如图,轨道旁边的测速仪测得弹珠1分钟末的速度为2米/分,求:
(1)二次函数和反比例函数的关系式.
(2)弹珠在轨道上行驶的最大速度.

【答案】(1)v=![]() (2<t≤5) (2)8米/分
(2<t≤5) (2)8米/分
【解析】分析:(1)由图象可知前一分钟过点(1,2),后三分钟时过点(2,8),分别利用待定系数法可求得函数解析式;
(2)把t=2代入(1)中二次函数解析式即可.
详解:(1)v=at2的图象经过点(1,2),
∴a=2.
∴二次函数的解析式为:v=2t2,(0≤t≤2);
设反比例函数的解析式为v=![]() ,
,
由题意知,图象经过点(2,8),
∴k=16,
∴反比例函数的解析式为v=![]() (2<t≤5);
(2<t≤5);
(2)∵二次函数v=2t2,(0≤t≤2)的图象开口向上,对称轴为y轴,
∴弹珠在轨道上行驶的最大速度在2秒末,为8米/分.
点睛:本题考查了反比例函数和二次函数的应用.解题的关键是从图中得到关键性的信息:自变量的取值范围和图象所经过的点的坐标.
【题型】解答题
【结束】
24
【题目】阅读材料:小胖同学发现这样一个规律:两个顶角相等的等腰三角形,如果具有公共的顶角的顶点,并把它们的底角顶点连接起来则形成一组旋转全等的三角形.小胖把具有这个规律的图形称为“手拉手”图形.如图1,在“手拉手”图形中,小胖发现若∠BAC=∠DAE,AB=AC,AD=AE,则BD=CE.
(1)在图1中证明小胖的发现;
借助小胖同学总结规律,构造“手拉手”图形来解答下面的问题:
(2)如图2,AB=BC,∠ABC=∠BDC=60°,求证:AD+CD=BD;
(3)如图3,在△ABC中,AB=AC,∠BAC=m°,点E为△ABC外一点,点D为BC中点,∠EBC=∠ACF,ED⊥FD,求∠EAF的度数(用含有m的式子表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图①所示是边长为![]() 的大正方形中有一个边长为
的大正方形中有一个边长为![]() 的小正方形.图②是由图①中阴影部分拼成的一个长方形.
的小正方形.图②是由图①中阴影部分拼成的一个长方形.

(1)设图①中阴影部分的面积为![]() ,图②中阴影部分的面积为
,图②中阴影部分的面积为![]() ,请用含
,请用含![]() 的式子表示:
的式子表示:![]() ,
,![]() ;(不必化简)
;(不必化简)
(2)以上结果可以验证的乘法公式是 ;
(3)利用(2)中得到的公式,计算:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 为等边三角形,
为等边三角形,![]() 为射线
为射线![]() 上一点,
上一点,![]() 为射线
为射线![]() 上一点,
上一点,![]() .
.
(1)如图1,当点![]() 在
在![]() 的延长线上且
的延长线上且![]() 时,
时,![]() 是
是![]() 的中线吗?请说明理由;
的中线吗?请说明理由;
(2)如图2,当点![]() 在
在![]() 的延长线上时,写出
的延长线上时,写出![]() 之间的数量关系,请说明理由;
之间的数量关系,请说明理由;
(3)如图3,当点![]() 在线段
在线段![]() 的延长线上,点
的延长线上,点![]() 在线段
在线段![]() 上时,请直接写出
上时,请直接写出![]() 的数量关系.
的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法“①凡正方形都相似;②凡等腰三角形都相似;③凡等腰直角三角形都相似;④直角三角形斜边上的中线与斜边的比为![]() ;⑤两个相似多边形的面积比为
;⑤两个相似多边形的面积比为![]() ,则周长的比为
,则周长的比为![]() .”中,正确的个数有( )个
.”中,正确的个数有( )个
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个边长分别为![]() 的正方形如图①放置,其未重合部分(阴影部分)面积为S1 . 在图①中大正方形的右下角摆放一个边长为b的小正方形,得到图②,两个边长为b的小正方形重合部分(阴影部分)面积为S2.
的正方形如图①放置,其未重合部分(阴影部分)面积为S1 . 在图①中大正方形的右下角摆放一个边长为b的小正方形,得到图②,两个边长为b的小正方形重合部分(阴影部分)面积为S2.
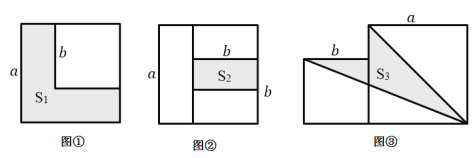
(1)用含a、b的代数式分别表示S1、S2.
(2)若a+b=9,ab=21,求S1+S2的值.
(3)将两个边长分别为a和b的正方形如图③放置.当S1+S2=30时,求出图③中阴影部分的面积S3.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com