
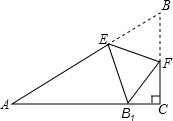
 如图,在△ABC中,∠ACB=90°,∠A=30°,AB=6,点E、F分别在AB、BC上,沿EF将△EBF翻折,使顶点B的对应点B1落在AC上,若EB1⊥AC,则EF等于
如图,在△ABC中,∠ACB=90°,∠A=30°,AB=6,点E、F分别在AB、BC上,沿EF将△EBF翻折,使顶点B的对应点B1落在AC上,若EB1⊥AC,则EF等于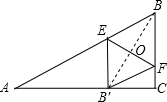 解:如图,连接BB′,交EF与点O;
解:如图,连接BB′,交EF与点O;| EO |
| FO |
| B′O |
| BO |


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:初中数学 来源: 题型:
 如图是一块长、宽、高分别是6cm,4cm和3cm的长方体木块.一只蚂蚁要从长方体木块的一个顶点A处,沿着长方体的表面到长方体上和A相对的顶点B处吃食物,那么它需要爬行的最短路径的长的平方是( )
如图是一块长、宽、高分别是6cm,4cm和3cm的长方体木块.一只蚂蚁要从长方体木块的一个顶点A处,沿着长方体的表面到长方体上和A相对的顶点B处吃食物,那么它需要爬行的最短路径的长的平方是( )| A、97 | B、109 | C、81 | D、85 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com