
【题目】已知关于x的一元二次方程|x2﹣1|=(x﹣1)(kx﹣2):
(1)若k=3,求方程的解;
(2)若方程恰有两个不同解,求实数k的取值范围.
【答案】(1)x1=![]() ,x2=1,x3=
,x2=1,x3=![]() ;(2)k≤0或k=1或k≥4.
;(2)k≤0或k=1或k≥4.
【解析】
(1)将k=3代入原方程,然后根据绝对值的性质把原方程化成两个一元二次方程进行解答;
(2)由于x=1恒为方程|x21|=(x1)(kx2)的解,当x≠1时,只需函数y=![]() 与函数y=kx2的图象只有一个交点就可以,画出x≠1时函数y=
与函数y=kx2的图象只有一个交点就可以,画出x≠1时函数y=![]() ,根据图象确定直线y=kx2与函数y=
,根据图象确定直线y=kx2与函数y=![]() 图象只有一个交点时,k的取值范围便可.
图象只有一个交点时,k的取值范围便可.
解:(1)把k=3代入|x2﹣1|=(x﹣1)(kx﹣2)中,得|x2﹣1|=(x﹣1)(3x﹣2),
当x2>1,即x>1或x<﹣1时,原方程可化为:x2﹣1=(x﹣1)(3x﹣2),
解得,x=1(舍),或x=![]() ;
;
当x2≤1,即﹣1≤x≤1时,原方程可化为:1﹣x2=(x﹣1)(3x﹣2),
解得,x=1,或x=![]() ;
;
综上,方程的解为x1=![]() ,x2=1,x3=
,x2=1,x3=![]() ;
;
(2)∵x=1恒为方程|x2﹣1|=(x﹣1)(kx﹣2)的解,
∴当x≠1时,方程两边都同时除以x﹣1得,![]() =kx﹣2,
=kx﹣2,
要使此方程只有一个解,只需函数y=![]() 与函数y=kx﹣2的图象只有一个交点.
与函数y=kx﹣2的图象只有一个交点.
∵函数: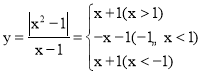 ,
,
作出函数图象,
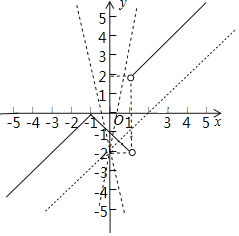
由图象可知,当k<0时,直线y=kx﹣2与函数y=![]() 图象只有一个交点;
图象只有一个交点;
当k=0时,直线y=kx﹣2=﹣2与函数y![]() 图象只有一个交点;
图象只有一个交点;
当k=1时,y=kx﹣2=x﹣2与y=x+1平行,则与函数y=![]() 图象只有一个交点;
图象只有一个交点;
∵当直线y=kx﹣2过(1,2)点时,2=k﹣2,则k=4,
∴函数图象可知,当k≥4时,直线y=kx﹣2与函数y=![]() 图象也只有一个交点,
图象也只有一个交点,
∴要使函数图象与y=kx﹣2图象有且只有一个交点,则实数k的取值范围是k≤0或k=1或k≥4.
综上,实数k的取值范围:k≤0或k=1或k≥4.


科目:初中数学 来源: 题型:
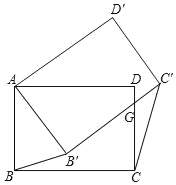
【题目】如图,将矩形ABCD绕点A按逆时针方向旋转一定角度后,BC的对应边B′C交CD边于点G,如果当AB′=B′G时量得AD=7,CG=4,连接BB′、CC′,那么![]() =_____.
=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
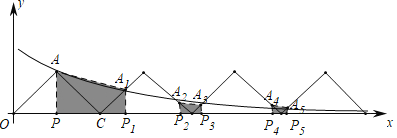
【题目】如图,在△AOC中,∠OAC=90°,AO=AC,OC=2,将△AOC放置于平面直角坐标系中,点O与坐标原点重合,斜边OC在x轴上.反比例函数y=![]() (x>0)的图象经过点A.将△AOC沿x轴向右平移2个单位长度,记平移后三角形的边与反比例函数图象的交点为A1,A2.重复平移操作,依次记交点为A3,A4,A5,A6…分别过点A,A1,A2,A3,A4,A5…作x轴的垂线,垂足依次记为P,P1,P2,P3,P4,P5…若四边形APP1A1的面积记为S1,四边形A2P2P3A3的面积记为S2…,则Sn=_____.(用含n的代数式表示,n为正整数)
(x>0)的图象经过点A.将△AOC沿x轴向右平移2个单位长度,记平移后三角形的边与反比例函数图象的交点为A1,A2.重复平移操作,依次记交点为A3,A4,A5,A6…分别过点A,A1,A2,A3,A4,A5…作x轴的垂线,垂足依次记为P,P1,P2,P3,P4,P5…若四边形APP1A1的面积记为S1,四边形A2P2P3A3的面积记为S2…,则Sn=_____.(用含n的代数式表示,n为正整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
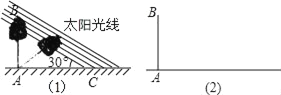
【题目】某数学兴趣小组,利用树影测量树高,如图(1),已测出树AB的影长AC为12米,并测出此时太阳光线与地面成30°夹角.
(1)求出树高AB;
(2)因水土流失,此时树AB沿太阳光线方向倒下,在倾倒过程中,树影长度发生了变化,假设太阳光线与地面夹角保持不变.求树的最大影长.(用图(2)解答)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B、C、D均在⊙O上,FB与⊙O相切于点B,AB与CF交于点G,OA⊥CF于点E,AC∥BF.
(1)求证:FG=FB.
(2)若tan∠F=![]() ,⊙O的半径为4,求CD的长.
,⊙O的半径为4,求CD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=﹣x2+2tx+2.
(1)求抛物线的对称轴(用含t的代数式表示);
(2)将点A(﹣1,3)向右平移5个单位长度,得到点B.
①若抛物线经过点B求t的值;
②若抛物线与线段AB恰有一个交点,结合函数图象直接写出t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,长方形ABCD(每个内角都是90°)的顶点的坐标分别是A(0,m),B(n,0),(m>n>0),点E在AD上,AE=AB,点F在y轴上,OF=OB,BF的延长线与DA的延长线交于点M,EF与AB交于点N.
(1)试求点E的坐标(用含m,n的式子表示);
(2)求证:AM=AN;
(3)若AB=CD=12cm,BC=20cm,动点P从B出发,以2cm/s的速度沿BC向C运动的同时,动点Q从C出发,以vcm/s的速度沿CD向D运动,是否存在这样的v值,使得△ABP与△PQC全等?若存在,请求出v值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】连接着汉口集家咀的江汉三桥(晴川桥),是一座下承式钢管混凝土系杆拱桥.它犹如一道美丽的彩虹跨越汉江,是江城武汉的一道靓丽景观.桥的拱肋ACB视为抛物线的一部分,桥面(视为水平的)与拱肋用垂直于桥面的系杆连接,相邻系杆之间的间距均为5米(不考虑系杆的粗细),拱肋的跨度AB为280米,距离拱肋的右端70米处的系杆EF的长度为42米.以AB所在直线为x轴,抛物线的对称轴为y轴建立如图②所示的平面直角坐标系.
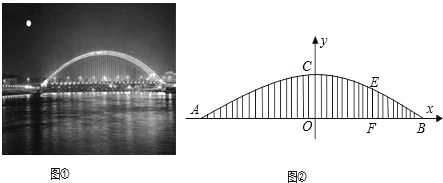
(1)求抛物线的解析式;
(2)正中间系杆OC的长度是多少米?是否存在一根系杆的长度恰好是OC长度的一半?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
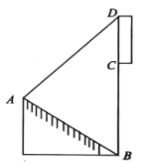
【题目】小明在某个斜坡![]() 上,看到对面某高楼
上,看到对面某高楼![]() 上方有一块宜传“中国国际进口博览会”的竖直标语牌
上方有一块宜传“中国国际进口博览会”的竖直标语牌![]() .小明在
.小明在![]() 点测得标语牌顶端D处的仰角为
点测得标语牌顶端D处的仰角为![]() ,并且测得斜坡
,并且测得斜坡![]() 的坡度为
的坡度为![]() (
(![]() 在同一条直线上),已知斜坡
在同一条直线上),已知斜坡![]() 长
长![]() 米,高楼高
米,高楼高![]() 米(即
米(即![]() 米),则标语牌
米),则标语牌![]() 的长是( )米.(结果保留小数点后一位)(参考数据:
的长是( )米.(结果保留小数点后一位)(参考数据:![]() ,
, ![]() ,
, ![]() ,
,![]() )
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com