
【题目】如图,在等腰直角三角形![]() 和
和![]() 中,点
中,点![]() 为它们的直角顶点,当
为它们的直角顶点,当![]() 与
与![]() 有重叠部分时:
有重叠部分时:
(1)①连接![]() ,如图1,求证:
,如图1,求证: ![]() ;
;
②连接![]() ,如图2,求证:
,如图2,求证: ![]() ;
;
(2)当![]() 与
与![]() 无重叠部分时:连接
无重叠部分时:连接![]() ,如图3,当
,如图3,当![]() ,
, ![]() 时,计算四边形
时,计算四边形![]() 面积的最大值,并说明理由.
面积的最大值,并说明理由.



【答案】(1) ①见解析;②见解析;(2)![]()
【解析】试题分析:(1)①利用同角的余角相等证出∠ACD=∠BCE,然后利用“SAS”证明△ACD≌△BCE即可得出结论;
②因为△ACE与△CDB的一条边AC=BC,所以要证两个三角形的面积相等只要证明AC和BC边上的高相等即可,过点E作EF⊥AC,过点D作DH⊥BC,通过证明△CEF≌△CDH即可得出结论;
(2)设△BCD的BC边上的高为h,同(1)②的方法可得S△ACE=S△BCD,所以S四边形ABDE=S△ABC+S△CDE+S△ACE+S△BCD=![]() +5h,而h≤CD,故当h=CD=2时S四边形ABDE最大,代入h=2求出最大值即可.
+5h,而h≤CD,故当h=CD=2时S四边形ABDE最大,代入h=2求出最大值即可.
试题解析:
解:(1)①∵∠ACD+∠BCD=90°,∠BCE+∠BCD=90°,
∴∠ACD=∠BCE,
又∵AC=BC,CD=CE,
∴△ACD≌△BCE(SAS),
∴AD=BE;
②如图:作EF⊥AC交AC的延长线于点F,作DH⊥BC于点H,
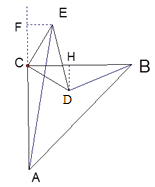
∵∠FCE+∠ECH=90°,∠HCD+∠ECH=90°,
∴∠FCE=∠HCD,
∵∠EFC=∠DHC=90°,CE=CD,
∴△CEF≌△CDH(AAS),
∴EF=DH,
∵S△ACE=![]() AC·EF,S△CDB=
AC·EF,S△CDB=![]() BC·DH,AC=BC,
BC·DH,AC=BC,
∴S△ACE=S△CDB;
(2)设△BCD的BC边上的高为h,
同(1)②的方法可得S△ACE=S△BCD,
∴S四边形ABDE=S△ABC+S△CDE+S△ACE+S△BCD=![]() ×52+
×52+![]() ×22+2 S△BCD =
×22+2 S△BCD =![]() +5h,
+5h,
∵h≤CD,
∴当h=CD=2时S四边形ABDE最大,
∴四边形ABDE的面积最大值为![]() +5×2=
+5×2=![]() .
.


科目:初中数学 来源: 题型:
【题目】某探测队在地面A、B两处均探测出建筑物下方C处有生命迹象,已知探测线与地面的夹角分别是25°和60°,且AB=4米,求该生命迹象所在位置C的深度.(结果精确到1米.参考数据:sin25°≈0.4,cos25°≈0.9,tan25°≈0.5,![]() ≈1.7)
≈1.7)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知顶点为(﹣3,﹣6)的抛物线y=ax2+bx+c经过点A,点(﹣2,m)和(﹣5,n)在该抛物线上,则下列结论中不正确的是( )
A.![]() >4ac
>4ac
B.m>n
C.方程a![]() +bx+c=﹣4的两根为﹣5或﹣1
+bx+c=﹣4的两根为﹣5或﹣1
D.a![]() +bx+c≥﹣6
+bx+c≥﹣6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明是个爱探究的学生,在学习完等腰三角形的判定定理之后,对于等腰![]() (如图甲),若
(如图甲),若![]() ,
,![]() ,小明发现,只要作
,小明发现,只要作![]() 的平分线就可以将
的平分线就可以将![]() 分成两个等腰三角形.
分成两个等腰三角形.
(1)你认为小明的发现正确吗?若正确,请给出证明过程;若不正确,请说明理由;
(2)请你对图乙的三角形进行探索,将![]() 分成两个等腰三角形,并写出顶角度数;
分成两个等腰三角形,并写出顶角度数;
(3)请你对图丙的三角形进行再探索,将![]() 分成三个等腰三角形,并写出顶角度数.
分成三个等腰三角形,并写出顶角度数.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】老师在课堂上出了一个问题:若点A(﹣2,y1),B(1,y2)和C(4,y3)都在反比例函数y=![]() 的图象上,比较y1 , y2 , y3的大小.
的图象上,比较y1 , y2 , y3的大小.
小明是这样思考的:当k<0时,反比例函数的图象是y随x的增大而增大的,并且﹣2<1<4,所以y1<y2<y3 .
你认为小明的思考 (填“正确”和“不正确”),理由是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
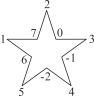
【题目】如图,将-2,-1,0,1,2,3,4,5,6,7这10个数分别填写在五角星中每两条线的交点处(每个交点处只填写一个数),将每一条线上的4个数相加,共得5个数,设为a1,a2,a3,a4,a5.
(1)求![]() (a1+a2+a3+a4+a5)的值;
(a1+a2+a3+a4+a5)的值;
(2)交换其中任何两位数的位置后,![]() (a1+a2+a3+a4+a5)的值是否改变?并说明理由.
(a1+a2+a3+a4+a5)的值是否改变?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】北京联合张家口成功申办2022年冬奥会后,滑雪运动已成为人们喜爱的娱乐健身项目.如图是某滑雪场为初学者练习用的斜坡示意图,出于安全因素考虑,决定将斜坡的倾角由45°降为30°,已知原斜坡坡面AB长为200米,点D,B,C在同一水平地面上,求改善后的斜坡坡角向前推进的距离BD.(结果保留整数.参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈2.45)
≈2.45)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B是直线m上两个定点,C是直线n上一个动点,且m∥n.以下说法:
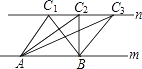
①△ABC的周长不变;
②△ABC的面积不变;
③△ABC中,AB边上的中线长不变.
④∠C的度数不变;
⑤点C到直线m的距离不变.
其中正确的有________(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)(x﹣1)(x+1)=x2﹣1,
(x﹣1)(x2+x+1)=x3﹣1,
(x﹣1)(x3+x2+x+1)= ,
…
猜想:(x﹣1)(xn+xn﹣1+…+x2+x+1)= ,
(2)根据以上结果,试写出下面两式的结果
①(x﹣1)(x49+x48+…+x2+x+1)= ,
②(x20﹣1)÷(x﹣1)= ,
(3)利用以上结论求值:1+3+32+33+34+……+32017
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com