
【题目】如图,AB为⊙O的直径,C为⊙O上一点,AD垂直于过点C的直线,垂足为D,且AC平分∠DAB,
(1)求证:DC是⊙O的切线;
(2)若⊙O的半径为2,AC=2![]() ,求线段AD的长;
,求线段AD的长;
(3)在(2)的条件下,求图中阴影部分的面积(直接写出答案).

【答案】(1)证明见解析;(2)AD=3;(3)![]()
【解析】
(1)连接OC,由OA=OC可以得到∠OAC=∠OCA,然后利用角平分线的性质可以证明∠DAC=∠OCA,接着利用平行线的判定即可得到OC∥AD,然后就得到OC⊥CD,由此即可证明直线CD与⊙O相切于C点;
(2)连接BC,根据圆周角定理的推理得到∠ACB=90°,又∠DAC=∠OAC,由此可以得到△ADC∽△ACB,然后利用相似三角形的性质即可解决问题;
(3)设AD交⊙O于点E,连接OE,根据S阴=S梯形AOCD-S△AOE-S扇形COE计算即可.
(1)证明:连接OC,
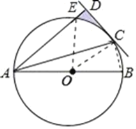
∵OA=OC
∴∠OAC=∠OCA
∵AC平分∠DAB
∴∠DAC=∠OAC
∴∠DAC=∠OCA
∴OC∥AD
∵AD⊥CD,
∴OC⊥CD,
∴DC是⊙O的切线;
(2)连接BC,
∵AB为⊙O的直径,
∴∠ACB=90°.
∵∠DAC=∠OAC,∠ADC=∠ACB=90°,
∴△ADC∽△ACB,
∴![]() ,
,
∵⊙O的半径为2,AC=2![]() ,
,
∴AD=3;
(3)∵AD⊥CD,
∴![]() ,
,
∵OC∥AD,
∴S梯形AOCD=![]() ,
,
在Rt△ABC中,AC=2![]() ,AB=4,
,AB=4,
∴![]() ,
,
∴∠BAC=30°,
∴∠BAD=60°,
设AD交⊙O于点E,连接OE,
∵OA=OE,
∴△AOE是等边三角形,
∴∠AOE=60°,
∵OC∥AD,
∴∠AOC=180°﹣∠BAD=120°,
∴∠COE=60°,
∴S阴=S梯形AOCD﹣S△AOE﹣S扇形COE=![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知△ABC,按以下步骤作图:①分别以B,C为圆心,以大于![]() BC的长为半径作弧,两弧相交于两点M,N;②作直线MN交直线AB于点D,连接CD.若∠ABC=40°,∠ACD=30°,则∠BAC的度数为_____.
BC的长为半径作弧,两弧相交于两点M,N;②作直线MN交直线AB于点D,连接CD.若∠ABC=40°,∠ACD=30°,则∠BAC的度数为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装超市购进单价为30元的童装若干件,物价部门规定其销售单价不低于每件30元,不高于每件60元.销售一段时间后发现:当销售单价为60元时,平均每月销售量为80件,而当销售单价每降低10元时,平均每月能多售出20件.同时,在销售过程中,每月还要支付其他费用450元.设销售单价为x元,平均月销售量为y件.
(1)求出y与x的函数关系式,并写出自变量x的取值范围.
(2)当销售单价为多少元时,销售这种童装每月可获利1800元?
(3)当销售单价为多少元时,销售这种童装每月获得利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
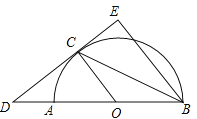
【题目】如图,已知AB是⊙O的直径,CD与⊙O相切于C,BE∥CO.
(1)求证:BC是∠ABE的平分线;
(2)若DC=8,⊙O的半径OA=6,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
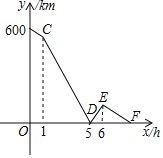
【题目】A、B两地之间为直线距离且相距600千米,甲开车从A地出发前往B地,乙骑自行车从B地出发前往A地,已知乙比甲晚出发1小时,两车均匀速行驶,当甲到达B地后立即原路原速返回,在返回途中再次与乙相遇后两车都停止,如图是甲、乙两人之间的距离s(千类)与甲出发的时间t(小时)之间的图象,则当甲第二次与乙相遇时,乙离B地的距离为_____千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD中,CD=4,BC=6,按以下步骤作图:①以点C为圆心,适当长度为半径作弧,分别交BC,CD于M,N两点:②分别以点M,N为圆心,以大于![]() MN的长为半径画弧,两弧在ABCD的内部交于点P;③连接CP并延长交AD于点E,交BA的延长线于点F,则AF的长为( )
MN的长为半径画弧,两弧在ABCD的内部交于点P;③连接CP并延长交AD于点E,交BA的延长线于点F,则AF的长为( )
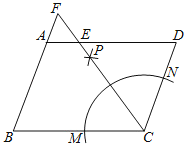
A.1B.2C.2.5D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】风电已成为我国继煤电、水电之后的第三大电源,风电机组主要由塔杆和叶片组成(如图1),图2是从图1引出的平面图.假设你站在A处测得塔杆顶端C的仰角是55°,沿HA方向水平前进43米到达山底G处,在山顶B处发现正好一叶片到达最高位置,此时测得叶片的顶端D(D、C、H在同一直线上)的仰角是45°.已知叶片的长度为35米(塔杆与叶片连接处的长度忽略不计),山高BG为10米,BG⊥HG,CH⊥AH,求塔杆CH的高.(参考数据:tan55°≈1.4,tan35°≈0.7,sin55°≈0.8,sin35°≈0.6)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年12月以来,湖北省武汉市部分医院陆续发现不明原因肺炎病例,现已证实该肺炎为一种新型冠状病毒感染的肺炎,其传染性较强.为了有效地避免交叉感染,需要采取以下防护措施:①戴口罩;②勤洗手;③少出门;④重隔离;⑤捂口鼻;⑥谨慎吃.某公司为了解员工对防护措施的了解程度(包括不了解、了解很少、基本了解和很了解),通过网上问卷调查的方式进行了随机抽样调查(每名员工必须且只能选择一项),并将调查结果绘制成如下两幅统计图.
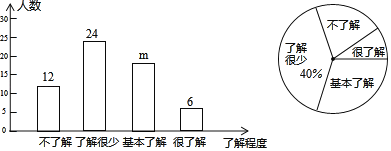
请你根据上面的信息,解答下列问题
(1)本次共调查了 名员工,条形统计图中m= ;
(2)扇形统计图中“很了解”扇形所对应的圆心角度数是_____________;
(3)若该公司共有员工1200名,请你估计不了解防护措施的人数;
(4)在调查中,发现有4名员工对防护措施很了解,其中有3名男员工、1名女员工.若准备从他们中随机抽取2名,让其在公司群内普及防护措施,求恰好抽中一男一女的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com