
分析 根据无理数、有理数的定义即可判定所给数中的无理数.
解答 解:-$\sqrt{5}$,π,0.202002…,cos45°=$\frac{\sqrt{2}}{2}$,属于无理数,
$\frac{22}{7}$,-$\sqrt{49}$=-7,tan45°=1,($\sqrt{2}$)0=1,(-$\frac{1}{2}$)-2=4,属于有理数,
故答案是:-$\sqrt{5}$,π,0.202002…,cos45°.
点评 此题主要考查了无理数的定义,注意带根号的要开不尽方才是无理数,无限不循环小数为无理数.如π,$\sqrt{6}$,0.8080080008…(每两个8之间依次多1个0)等形式.


科目:初中数学 来源: 题型:解答题
 如图,已知?ABCD,AB=$\frac{1}{2}$BC,延长AB至F,使BF=AB,再延长BA至E,使AE=AB,试判断EC与FD的位置关系,并说明其结论正确的理由.
如图,已知?ABCD,AB=$\frac{1}{2}$BC,延长AB至F,使BF=AB,再延长BA至E,使AE=AB,试判断EC与FD的位置关系,并说明其结论正确的理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
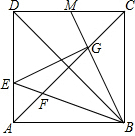 如图,在边长为6的正方形ABCD中,点E为边AD上的一个动点(与点A、D不重合),∠EBM=45°,BE交对角线AC于点F,BM交于AC于点G,交CD于点M.
如图,在边长为6的正方形ABCD中,点E为边AD上的一个动点(与点A、D不重合),∠EBM=45°,BE交对角线AC于点F,BM交于AC于点G,交CD于点M.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
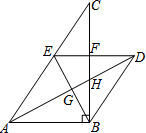 如图,在△ABC中,∠ABC=90°,过点B作AC的平行线交∠CAB的平分线于点D,过点D作AB的平行线交AC于点E,交BC于点F,连接BE,交AD于点G.
如图,在△ABC中,∠ABC=90°,过点B作AC的平行线交∠CAB的平分线于点D,过点D作AB的平行线交AC于点E,交BC于点F,连接BE,交AD于点G.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
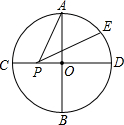 如图,AB与CD是半径为1的⊙O互相垂直的两直径,E为弧AD的三等分点(点E距点D近),P是直径CD上一动点,则PA+PE的最小值为$\sqrt{3}$.
如图,AB与CD是半径为1的⊙O互相垂直的两直径,E为弧AD的三等分点(点E距点D近),P是直径CD上一动点,则PA+PE的最小值为$\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com