
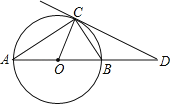
【题目】已知:如图AB为⊙O直径,C是⊙O上一点,D在AB的延长线上,∠DCB=∠A.
(1)求证:CD是⊙O的切线.
(2)若CD与⊙O相切,且∠D=30°,BD=10,求⊙O的半径.
科目:初中数学 来源: 题型:
【题目】某地2016年为做好“精准扶贫”,投入资金1000万元用于异地安置,并规划投入资金逐年增加,2018年在2016年的基础上增加投入资金1250万元.
(1)从2016年到2018年,该地投入异地安置资金的年平均增长率为多少?
(2)在2018年异地安置的具体实施中,该地计划投入资金不低于400万元用于优先搬迁租房奖励,规定前1000户(含第1000户)每户每天奖励8元,1000户以后每户每天补助5元,按租房400天计算,试求今年该地至少有多少户享受到优先搬迁租房奖励?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列两个三角形不一定相似的是
A.两条直角边的比都是![]() 的两个直角三角形
的两个直角三角形
B.腰与底的比都是![]() 的两个等腰三角形
的两个等腰三角形
C.有一个内角为![]() 的两个直角三角形
的两个直角三角形
D.有一个内角为![]() 的两个等腰三角形
的两个等腰三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个盒子中装有1个红球、1个白球和2个蓝球,这些球除颜色外都相同.
(1)从盒子中任意摸出一个球,恰好是白球的概率是 ;
(2)从中随机摸出一个球,记下颜色后不放回,再从中随机摸出一个球,试用树状图或表格列出所以可能的结果,并求两次摸到的球的颜色能配成紫色的概率.(红色和蓝色在一起可配成紫色)
(3)往盒子里面再放入一个白球,如果从中随机摸出一个球,记下颜色后放回,再从中随机摸出一个球,那么两次摸到的球的颜色能配成紫色的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小飞设计的“过圆外一点作圆的切线”的尺规作图过程.
已知:P为⊙O外一点.
求作:经过点P的⊙O的切线.

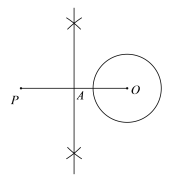
作法:如图,
①连接OP,作线段OP的垂直平分线交OP于点A;
②以点A为圆心,OA的长为半径作圆,交⊙O于B,C两点;
③作直线PB,PC.所以直线PB,PC就是所求作的切线.
根据小飞设计的尺规作图过程,
(1)使用直尺和圆规补全图形(保留作图痕迹);
(2)完成下面的证明(说明:括号里填写推理的依据).
证明:连接![]() ,
,![]() ,
,
∵![]() 为⊙
为⊙![]() 的直径,
的直径,
∴![]() ( ).
( ).
∴![]() ,
,![]() .
.
∴![]() ,
,![]() 为⊙
为⊙![]() 的切线( ).
的切线( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠BAC=∠ADE=90°,AD⊥BC,AC=DC.关于优弧CAD,下列结论正确的是( )

A.经过点B和点EB.经过点B,不一定经过点E
C.经过点E,不一定经过点BD.不一定经过点B和点E
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为2,点E是BC的中点,AE与BD交于点P,F是CD上的一点,连接AF分别交BD,DE于点M,N,且AF⊥DE,连接PN,则下列结论中:

①![]() ;②
;②![]() ;③tan∠EAF=
;③tan∠EAF=![]() ;④
;④![]() 正确的是()
正确的是()
A. ①②③B. ①②④C. ①③④D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店销售一种商品,经市场调查发现:该商品的月销售量y(件)是售价x(元/件)的一次函数,其售价x、月销售量y、月销售利润w(元)的部分对应值如下表:
售价x(元/件) | 40 | 45 |
月销售量y(件) | 300 | 250 |
月销售利润w(元) | 3000 | 3750 |
注:月销售利润=月销售量×(售价-进价)
(1)①求y关于x的函数表达式;
②当该商品的售价是多少元时,月销售利润最大?并求出最大利润;
(2)由于某种原因,该商品进价提高了m元/件(m>0),物价部门规定该商品售价不得超过40元/件,该商店在今后的销售中,月销售量与售价仍然满足(1)中的函数关系.若月销售最大利润是2400元,则m的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC 中,点 D 是线段 BC 上一点.作射线 AD ,点 B 关于射线 AD 的对称点为 E .连接 EC 并延长,交射线 AD 于点 F .
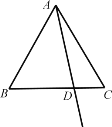
(1)补全图形;(2)求∠AFE 的度数;(3)用等式表示线段 AF 、CF 、 EF 之间的数量关系,并证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com