
����Ŀ��ij��2016��Ϊ����������ƶ����Ͷ���ʽ�1000��Ԫ������ذ��ã����滮Ͷ���ʽ��������ӣ�2018����2016��Ļ���������Ͷ���ʽ�1250��Ԫ��
��1����2016�굽2018�꣬�õ�Ͷ����ذ����ʽ����ƽ��������Ϊ���٣�
��2����2018����ذ��õľ���ʵʩ�У��õؼƻ�Ͷ���ʽ���400��Ԫ�������Ȱ�Ǩ�ⷿ�������涨ǰ1000��������1000����ÿ��ÿ�콱��8Ԫ��1000���Ժ�ÿ��ÿ�첹��5Ԫ�����ⷿ400����㣬�������õ������ж��ٻ����ܵ����Ȱ�Ǩ�ⷿ������
���𰸡���1����2016�굽2018�꣬�õ�Ͷ����ذ����ʽ����ƽ��������Ϊ50%����2������õ�������1400�����ܵ����Ȱ�Ǩ�ⷿ������
��������
��1��������2016��Ͷ���ʽ�![]()
![]() ��Ͷ���ʽ����з�����⼴��;
��Ͷ���ʽ����з�����⼴��;
��2���������⣬���ܽ����İ�Ǩ����Ϊǰ1000����1000��֮��IJ��֣��������Ǩ������Ϊ![]() ������ǰ1000�����ܽ����ܶ�+1000��֮�����ܽ����ۺϡ�400��Ԫ���ݴ˿ɽ�.
������ǰ1000�����ܽ����ܶ�+1000��֮�����ܽ����ۺϡ�400��Ԫ���ݴ˿ɽ�.
�⣺��1����õ�Ͷ����ذ����ʽ����ƽ��������Ϊx���������⣬
�ã�1000��1+x��2��1250+1000��
��ã�x��0.5��x����2.5���ᣩ��
�𣺴�2016�굽2018�꣬�õ�Ͷ����ذ����ʽ����ƽ��������Ϊ50%��
��2�������õ���a�����ܵ����Ȱ�Ǩ�ⷿ�������������⣬
�ã�1000��8��400+��a��1000����5��400��4000000��
��ã�a��1400��
�𣺽���õ�������1400�����ܵ����Ȱ�Ǩ�ⷿ������


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У��߳�Ϊ3��������ABCD�ڵ�һ�����ڣ�AB��x�ᣬ��A������Ϊ��5��4��������O����C��ֱ��l����ֱ��l��y������ƽ�ƣ�
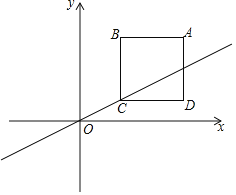
��1����ֱ��l��������ABCDֻ��һ��������ʱ����ֱ��l�Ľ���ʽ��
��2����ֱ��l��ƽ�ƹ�����ǡ��ƽ��������ABCD�����ʱ��ֱ��l�ֱ���x�ᡢy���ཻ�ڵ�E����F������BE��BF������BEF�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
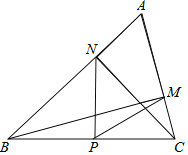
����Ŀ����ͼ�ڡ�ABC�С�A��60�㣬BM��AC�ڵ�M��CN��AC�ڵ�N��PΪBC�ߵ��е㣬����PM��PN�������н��ۣ���PM��PN����![]() ������PMNΪ�ȱ������Σ�������ABC��45��ʱ��BN��
������PMNΪ�ȱ������Σ�������ABC��45��ʱ��BN��![]() BC��������ȷ���ǣ�������
BC��������ȷ���ǣ�������
A.�٢ڢ�B.�٢ڢ�C.�٢ۢ�D.�ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
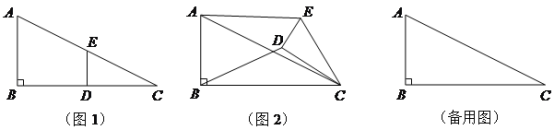
����Ŀ����10�֣���ͼ1����Rt��ABC�У���B=90����BC=2AB=8����D��E�ֱ��DZ�BC��AC���е㣬����DE. ����EDC�Ƶ�C��˳ʱ�뷽����ת������ת��Ϊ��.
��1�����ⷢ��
�� ��![]() ʱ��
ʱ��![]() ���� ��
���� ��![]() ʱ��
ʱ��![]()
��2����չ̽��
���жϣ���0��ܦ���360��ʱ��![]() �Ĵ�С���ޱ仯�������ͼ2���������֤��.
�Ĵ�С���ޱ仯�������ͼ2���������֤��.
��3��������
����EDC��ת��A��D��E���㹲��ʱ��ֱ��д���߶�BD�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������y��x2+bx+c��x���ཻ��A����1��0����B��m��0�����㣬��y���ཻ�ڵ�C��0����3���������ߵĶ���ΪD��
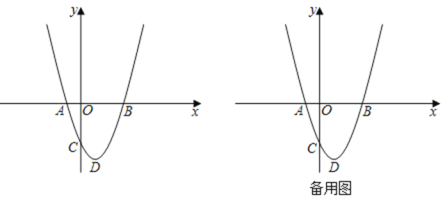
��1����B��D��������ꣻ
��2����P��ֱ��BC�·�������������һ�㣬����P��PH��x���ڵ�H����BC���ڵ�M����FΪy��һ���㣬���߶�PM�������ʱ����PH+HF+![]() CF����Сֵ��
CF����Сֵ��
��3���ڵڣ�2�����У���PH+HF+![]() CFȡ����Сֵʱ������OHF�Ƶ�O˳ʱ����ת60����õ���OH��F��������F����OF���Ĵ�����x�ύ�ڵ�Q����RΪ�����߶Գ����ϵ�һ�㣬��ƽ��ֱ������ϵ���Ƿ���ڵ�S��ʹ�õ�D��Q��R��SΪ������ı���Ϊ���Σ������ڣ���ֱ��д����S�����꣬�������ڣ���˵�����ɣ�
CFȡ����Сֵʱ������OHF�Ƶ�O˳ʱ����ת60����õ���OH��F��������F����OF���Ĵ�����x�ύ�ڵ�Q����RΪ�����߶Գ����ϵ�һ�㣬��ƽ��ֱ������ϵ���Ƿ���ڵ�S��ʹ�õ�D��Q��R��SΪ������ı���Ϊ���Σ������ڣ���ֱ��д����S�����꣬�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�������IJ�����װ��3������1��2��3��С�����ǵ���״����С��ȫ��ͬ����ǿ�Ӳ��������ȡ��һ��С��������Ϊx��Ȼ��Żش��н��ȣ������ٴӴ������ȡ��һ��С��������Ϊy������ȷ���˵�M�����꣨x��y����
��1�����б�����״ͼ��ֻѡ����һ�֣��ķ�����ʾ����M���п��ܵ����ꣻ
��2�����M��x��y���ں���y��x2ͼ���ϵĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������![]() ƽ�ƺ��������߾���ԭ�����ߵĶ���
ƽ�ƺ��������߾���ԭ�����ߵĶ���![]() ������������
������������![]() �������ύ�ڵ�
�������ύ�ڵ�![]() ������
������![]() ��
��![]() ��������������
��������������![]() �����һ������
�����һ������![]() ���������ߵĶ�����
���������ߵĶ�����![]() .
.
��1�����![]() �����ꣻ
�����ꣻ
��2�����![]() �����������ϣ�����
�����������ϣ�����![]() �����
�����![]() ƽ��
ƽ��![]() �����
�����![]() �����ꣻ
�����ꣻ
��3���ڣ�2���������£���������![]() ��
��![]() ������ƽ�ƣ���
������ƽ�ƣ���![]() �Ķ�Ӧ��Ϊ
�Ķ�Ӧ��Ϊ![]() ����
����![]() ��
��![]() ����ʱ����ֱ��д��ƽ�ƺ�õ������ߵı���ʽ.
����ʱ����ֱ��д��ƽ�ƺ�õ������ߵı���ʽ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ���������ڼ���ȫУѧ�������黭��Ʒ����������ʦ��ȫУ�����ȡ���ĸ��༶����A��B��C��D��������������Ʒ�����������˷���ͳ�ƣ�����������������������ͳ��ͼ��
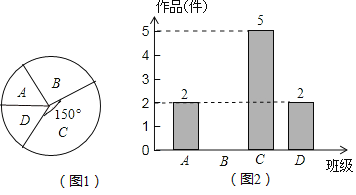
��1������ʦ�����ĸ��༶����������Ʒ���ټ���
��2�����ͼ2������ͳ��ͼ����������
��3����ȫУ��չ��Ʒ��������ͬѧ���һ�Ƚ�����������������������Ů��������Ҫ�����г�����ͬѧȥ�μ�ѧУ�ܽ������̸�ᣬ���û���״ͼ���б��ķ�����ǡ�ó���һ������һ��Ů���ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
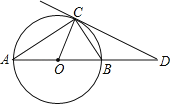
����Ŀ����֪����ͼABΪ��Oֱ����C�ǡ�O��һ�㣬D��AB���ӳ����ϣ���DCB����A��
��1����֤��CD�ǡ�O�����ߣ�
��2����CD���O���У��ҡ�D��30����BD��10�����O�İ뾶��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com