
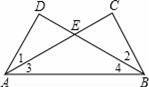
如图,给出下列论断:①DE=CE,②∠1=∠2,③∠3=∠4.请你将其中的两个作为条件,另一个作为结论,构成一个真命题,并加以证明.

【考点】全等三角形的判定与性质.
【专题】证明题;压轴题;开放型.
【分析】可以有三个真命题:
(1)②③⇒①,可由ASA证得△ADE≌△BCE,所以DE=EC;
(2)①③⇒②,可由SAS证得△ADE≌△BCE,所以∠1=∠2;
(3)①②⇒⑧,可由ASA证得△ADE≌△BCE,所以AE=BF,∠3=∠4.
【解答】解:②③⇒①
证明如下:
∵∠3=∠4,
∴EA=EB.
在△ADE和△BCE中,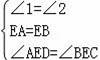

∴△ADE≌△BCE.
∴DE=EC.
①③⇒②
证明如下:
∵∠3=∠4,
∴EA=EB,
在△ADE和△BCE中,
 ,
,
∴△ADE≌△BCE,
∴∠1=∠2.
①②⇒⑧
证明如下:
在△ADE和△BCE中,
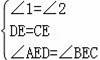

∴△ADE≌△BCE.
∴AE=BE,∠3=∠4.
【点评】本题考查了全等三角形的判定和性质;题目是一道开放型的问题,选择有多种,可以采用多次尝试法,证明时要选择较为简单的进行证明.


 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:
为节约能源,某单位按以下规定收取每月电费:用电不超过140度,按每度0.45元收费,如果超过140度,超过部分按每度0.60元收费.
(1)若某住户四月份的用电量是a度,求这个用户四月份应交多少电费?
(2)若该住户五月份的用电量是200度,则他五月份应交多少电费?
查看答案和解析>>
科目:初中数学 来源: 题型:
若点P关于x轴的对称点为P1(2a+b,3),关于y轴的对称点为P2(9,b+2),则点P的坐标为( )
A.(9,3) B.(﹣9,3) C.(9,﹣3) D.(﹣9,﹣3)
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,点A在BE上,且AC=AB,BD=CE.CE,BD交于点F,AC,BD交于点G.∠CAB=∠DFE.则AE等于( )
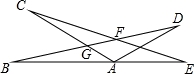
A.AD B.DF C.CE﹣AB D.BD﹣AB
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com