
【题目】如图,将矩形![]() 沿对角线
沿对角线![]() 剪开,再把
剪开,再把![]() 沿
沿![]() 方向平移得到
方向平移得到![]() ,连接
,连接![]() ,
,![]() ,若
,若![]() ,
,![]() ,
,![]() ,
,![]() 与
与![]() 重叠部分的面积为
重叠部分的面积为![]() ,则下列结论:①
,则下列结论:①![]() ;②当
;②当![]() 时,四边形
时,四边形![]() 是菱形;③当
是菱形;③当![]() 时,
时,![]() 为等边三角形;④
为等边三角形;④![]() .其中正确的有( )
.其中正确的有( )

A.1个B.2个C.3个D.4个
【答案】C
【解析】
①正确,根据SSS即可判断;
②正确,证明四边相等即可解决问题;
③正确,只要证明BD=DD1,∠BDD1=60°即可;
④错误,利用三角形的面积公式计算即可判定;
∵AC=A1C1,
∴AA1=CC1
∵BC=D1A1,∠AA1D1=∠BCC1,
∴△A1AD1≌△CC1B,故①正确,
在Rt△ABC中,∵∠ACB=30°,AB=1,
∴AC=A1C1=2,
当x=1时,AC1=CC1=1,
∴AC1=AB,
∵∠BAC=60°,
∴△ABC1是等边三角形,
同法可证:△AD1C1是等边三角形,
∴AB=BC1=AC1=AD1=C1D1,
∴四边形ABC1D1是菱形,故②正确,
当x=2时,BD=AC=2,DD1=2,∠BDD1=60°,
∴△BDD1是等边三角形,故③正确,
当0<x<2时,S=![]() (2-x)2,故④错误.
(2-x)2,故④错误.
故选:C.


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案科目:初中数学 来源: 题型:
【题目】五一期间,某商场计划购进甲、乙两种商品,已知购进甲商品1件和乙商品3件共需240元;购进甲商品2件和乙商品1件共需130元.
(1)求甲、乙两种商品每件的进价分别是多少元?
(2)商场决定甲商品以每件40元出售,乙商品以每件90元出售,为满足市场需求,需购进甲、乙两种商品共100件,且甲种商品的数量不少于乙种商品数量的4倍,请你求出获利最大的进货方案,并确定最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,一枚质地均匀的正四面体骰子,它有四个面并分别标有数字
,一枚质地均匀的正四面体骰子,它有四个面并分别标有数字![]() ,
,![]() ,
,![]() ,
,![]() ,如图
,如图![]() ,正方形
,正方形![]() 顶点处各有一个圈.跳圈游戏的规则为:游戏者每掷一次骰子,骰子着地一面上的数字是几,就沿正方形的边顺时针方向连续跳几个边长.如:若从图
顶点处各有一个圈.跳圈游戏的规则为:游戏者每掷一次骰子,骰子着地一面上的数字是几,就沿正方形的边顺时针方向连续跳几个边长.如:若从图![]() 起跳,第一次掷得
起跳,第一次掷得![]() ,就顺时针连续跳
,就顺时针连续跳![]() 个边长,落到圈
个边长,落到圈![]() ;若第二次掷得
;若第二次掷得![]() ,就从
,就从![]() 开始顺时针连续跳
开始顺时针连续跳![]() 个边长,落到圈
个边长,落到圈![]() ;
;![]() 设游戏者从圈
设游戏者从圈![]() 起跳.
起跳.
(![]() )嘉嘉随机掷一次骰子,求落回到圈
)嘉嘉随机掷一次骰子,求落回到圈![]() 的概率
的概率![]() .
.
(![]() )淇淇随机掷两次骰子,用列表法求最后落回到圈
)淇淇随机掷两次骰子,用列表法求最后落回到圈![]() 的概率
的概率![]() ,并指出她与嘉嘉落回到圈
,并指出她与嘉嘉落回到圈![]() 的可能性一样吗?
的可能性一样吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】程序框图的算法思路源于我国古代数学名著《九章算术》,如图所示的程序框图,当输入x的值是17时,根据程序,第一次计算输出的结果是10,第二次计算输出的结果是5,……,这样下去第2019次计算输出的结果是( )
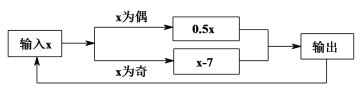
A.-2B.-1C.-8D.-4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“端午节”又称为端阳节、重午节、龙舟节、正阳节、洛兰节等,是中国四大传统节日之一,端午习俗众多,其中吃粽子是端午节的习俗主题之一,某超市5月以50元/盒的进价购进一款粽子1000盒,以100元/盒的售价全部销售完.销售人员根据市场调研预测,该款粽子每盒的售价在5月售价基础上每降价5元,月销量就会相应增加100盒,该超市6月计划购进该款粽子不超过1400盒.
(1)根据该超市6月计划,该款粽子6月的售价最少每盒可以定价多少元?
(2)实际上,6月该超市购进该款粽子的进价比5月便宜了![]() 元,而实际售价在5月基础上降了m元,已知6月的销售利润比5月增加8%,求m的值.
元,而实际售价在5月基础上降了m元,已知6月的销售利润比5月增加8%,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
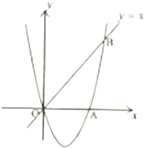
【题目】如图,经过原点![]() 的抛物线
的抛物线![]() 与
与![]() 轴交于另一点
轴交于另一点![]() ,在第一象限内与直线
,在第一象限内与直线![]() 交于点
交于点![]() .
.
(1)求这条抛物线的解析式;
(2)在第四象限内的抛物线上有一点![]() ,满足以
,满足以![]() ,
,![]() ,
,![]() 为顶点的三角形的面积为1,求点
为顶点的三角形的面积为1,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校计划厂家购买A、B两种型号的电脑,已知每台A种型号电脑比每台B种型号电脑多01.万元,且用10万元购买A种型号电脑的数量与用8万元购买B种型号电脑的数量相同;
(1)求A、B两种型号电脑单价各为多少万元?
(2)学校预计用不多于9.2万元的资金购进20台电脑,其中A种型号电脑至少要购进10台,请问有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
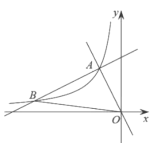
【题目】如图,在平面直角坐标系![]() 中,一次函数
中,一次函数![]() 和
和![]() 的图象相交于点
的图象相交于点![]() ,反比例函数
,反比例函数![]() 的图象经过点
的图象经过点![]() .
.
(1)求反比例函数的表达式;
(2)设一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象的另一个交点为
的图象的另一个交点为![]() ,连接
,连接![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com