
【题目】将一块直角三角板的直角顶点绕着矩形![]() (
(![]() )对角线交点
)对角线交点![]() 旋转(如图①→②→③),
旋转(如图①→②→③),![]() 、
、![]() 分别为直角三角板的直角边与矩形
分别为直角三角板的直角边与矩形![]() 的边
的边![]() 、
、![]() 的交点.
的交点.
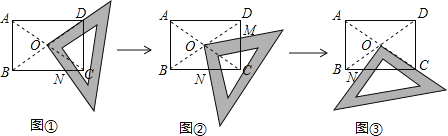
(1)发现:在图①中,当三角板的一直角边与![]() 重合,易证
重合,易证![]() ,
,
证明方法如下:连接![]() ,
,
∵![]() 为矩形
为矩形
∴![]()
又∵![]()
∴![]()
又∵![]()
∴![]()
∴![]()
在图③中,当三角板的一直角边与![]() 重合,求证:
重合,求证:![]() .
.
(2)根据以上学习探究:图②中![]() 、
、![]() 、
、![]() 、
、![]() 这四条线段之间的数量关系,写出你的结论,并说明理由.
这四条线段之间的数量关系,写出你的结论,并说明理由.
【答案】(1)见详解;(2)BN2+DM2=CM2+CN2,理由见详解
【解析】
(1)连接![]() ,由中垂线的性质得
,由中垂线的性质得![]() ,由勾股定理得
,由勾股定理得![]() ,进而即可得到结论;
,进而即可得到结论;
(2)延长NO交AD于点P,连接PM,MN,易证△BON≌△DOP,结合中垂线的性质得PM=MN,由勾股定理得PM2=PD2+DM2,MN2=CM2+CN2,进而即可得到结论.
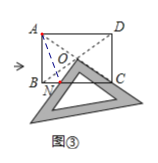
(1)连接![]() ,如图③,
,如图③,
∵四边形![]() 为矩形,
为矩形,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∵AB=CD,
∴![]() ;
;
(2)BN2+DM2=CM2+CN2,理由如下:
如图②,延长NO交AD于点P,连接PM,MN,
∵四边形ABCD是矩形,
∴OD=OB,AD∥BC,
∴∠DPO=∠BNO,∠PDO=∠NBO,
在△BON和△DOP中,
∵ ,
,
∴△BON≌△DOP(AAS),
∴ON=OP,BN=PD,
∵∠MON=90°,即:OM是线段PN的中垂线,
∴PM=MN,
∵∠PDM=∠NCM=90°,
∴PM2=PD2+DM2,MN2=CM2+CN2,
∴PD2+DM2=CM2+CN2,
∴BN2+DM2=CM2+CN2.



 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:初中数学 来源: 题型:
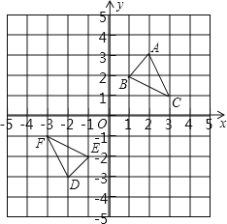
【题目】如图,△DEF是△ABC经过某种变换得到的图形,点A与点D,点![]() 与点E,点
与点E,点![]() 与点F分别是对应点,观察点与点的坐标之间的关系,解答下列问题:
与点F分别是对应点,观察点与点的坐标之间的关系,解答下列问题:
(1)分别写出点A与点D,点![]() 与点E,点
与点E,点![]() 与点F的坐标,并说说对应点的坐标有哪些特征;
与点F的坐标,并说说对应点的坐标有哪些特征;
(2)若点![]() 与点
与点![]() 也是通过上述变换得到的对应点,求
也是通过上述变换得到的对应点,求![]() 、b的值
、b的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 的算术平方根是3,
的算术平方根是3,![]() 的立方根是-2.
的立方根是-2.
(1)求![]() 和
和![]() 的值.
的值.
(2)用四则运算的加、减、乘、除定义一个新运算:![]() .
.
①若![]() ,
,![]() 2
2![]() ,判断点P(-
,判断点P(-![]() ,-
,-![]() )在第几象限?
)在第几象限?
②若![]() 满足
满足![]() ,且3
,且3![]() ,化简
,化简![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,点 D 是边 BC 上的点(与 B、C 两点不重合),过点 D作 DE∥AC,DF∥AB,分别交 AB、AC 于 E、F 两点,下列说法正确的是( )
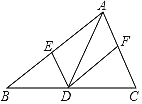
A. 若 AD 平分∠BAC,则四边形 AEDF 是菱形
B. 若 BD=CD,则四边形 AEDF 是菱形
C. 若 AD 垂直平分 BC,则四边形 AEDF 是矩形
D. 若 AD⊥BC,则四边形 AEDF 是矩形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里装有黑、白两种颜色的球共50个,这些球除颜色外其余完全相同.王颖做摸球试验,搅匀后,她从盒子里随机摸出一个球记下颜色后,再把球放回盒子中,不断重复上述过程,下表是试验中的一组统计数据:
摸球的次数 | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
摸到白球的次数 | 65 | 124 | 178 | 302 | 480 | 601 | 1800 |
摸到白球的频率 |
|
|
|
|
|
|
|
(1)若从盒子里随机摸出一个球,则摸到白球的概率的估计值为______.
(2)试估算盒子里黑、白两种颜色的球各有多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个大小一样的直角三角形重叠在一起,将其中一个三角形沿着点B到点C的方向平移到△DEF的位置,AB=10,DH=4,平移距离为6,则阴影部分面积是_____
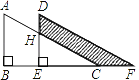
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用1块A型钢板可制成1块C型钢板、3块D型钢板;用1块B型钢板可制成2块C型钢板、1块D型钢板.
(1)现需150块C型钢板、180块D型钢板,则怡好用A型、B型钢板各多少块?
(2)若A、B型钢板共100块,现需C型钢板至多150块,D型钢板不超过204块,共有几种方案?
(3)若需C型钢板80块,D型钢板不多于45块(A型、B型钢板都要使用).求A、B型钢板各需多少块?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com