
����Ŀ����һ�������ĺ�����װ�кڡ���������ɫ����50������Щ�����ɫ��������ȫ��ͬ����ӱ���������飬���Ⱥ����Ӻ������������һ���������ɫ���ٰ���Żغ����У������ظ��������̣��±��������е�һ��ͳ�����ݣ�
����Ĵ��� | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
��������Ĵ��� | 65 | 124 | 178 | 302 | 480 | 601 | 1800 |
���������Ƶ�� |
|
|
|
|
|
|
|
��1�����Ӻ������������һ��������������ĸ��ʵĹ���ֵΪ______��
��2���Թ��������ڡ���������ɫ������ж��ٸ���
���𰸡���1��![]() ����2�����������ɫ������20ֻ������ɫ������30ֻ
����2�����������ɫ������20ֻ������ɫ������30ֻ
��������
��1�����⿼������Ƶ�ʹ��Ƹ�������ȡ�������µ�Ƶ��ֵ��Ϊ���ʹ���ֵ���
��2�����⿼�����ø���������������������չ�ʽ�����⼴�ɣ�
��1��������������ʱ������Ϊ3000��ʱ�����������Ƶ��Ϊ0.6������Ϊ����ʹ���ֵ��
��2���ڰ�����50ֻ��
����Ϊ��![]() ��ֻ����
��ֻ����
����Ϊ��![]() ��ֻ����
��ֻ����
�𣺺��������ɫ������20ֻ������ɫ������30ֻ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
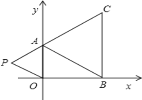
����Ŀ����ͼ��������ֱ������ϵ�У���֪A��0��a����B��b��0����C��b��c�����㣬����a��b��c�����ϵʽ![]() ��
��
��1����a��b��c��ֵ��
��2������ڵڶ���������һ��P��m��![]() �������ú�m��ʽ�ӱ�ʾ�ı���ABOP�������
�������ú�m��ʽ�ӱ�ʾ�ı���ABOP�������
��3���ڣ�2���������£��Ƿ���ڵ�P��ʹ�ı���ABOP��������ABC�������ȣ������ڣ������P�����꣬�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��D��E�ֱ��ǡ�ABC��AB��BC�ϵĵ㣬AD��2BD��BE��CE�����ADF�����ΪS1����CEF�����ΪS2����S1��S2��a����S��ABC��_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ��ֱ�����ǰ��ֱ�Ƕ������ž���![]() ��
��![]() ���Խ��߽���
���Խ��߽���![]() ��ת����ͼ�١��ڡ��ۣ���
��ת����ͼ�١��ڡ��ۣ���![]() ��
��![]() �ֱ�Ϊֱ�����ǰ��ֱ�DZ������
�ֱ�Ϊֱ�����ǰ��ֱ�DZ������![]() �ı�
�ı�![]() ��
��![]() �Ľ��㣮
�Ľ��㣮
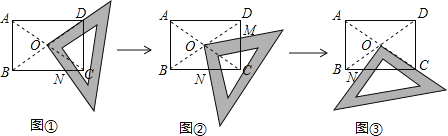
��1�����֣���ͼ���У������ǰ��һֱ�DZ���![]() �غϣ���֤
�غϣ���֤![]() ��
��
֤���������£�����![]() ��
��
��![]() ����
����
��![]()
�֡�![]()
��![]()
�֡�![]()
��![]()
��![]()
��ͼ���У������ǰ��һֱ�DZ���![]() �غϣ���֤��
�غϣ���֤��![]() ��
��
��2����������ѧϰ̽����ͼ����![]() ��
��![]() ��
��![]() ��
��![]() �������߶�֮���������ϵ��д����Ľ��ۣ���˵�����ɣ�
�������߶�֮���������ϵ��д����Ľ��ۣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2016�깲��������ճ��������õؽ�������ǡ����һ��������ѵ����⣮��ֹ��2016��ף���ofo������������Ͷ�������ǡ�Ħ�ݵ�����Ͷ��������1.6�������dz���ҲԶ���ڡ�Ħ�ݵ���������ofo����������ע���û���ԼΪ960���ˣ���Ħ�ݵ�������ע���û���ԼΪ750���ˣ���ͳ��ʹ��һ����ofo������������ƽ��������ʹ��һ����Ħ�ݵ�������ƽ��������3�ˣ�����ע�������ֵ������û�����ʹ�ù�����������2016�ꡰĦ�ݵ�������Ͷ������ԼΪ������̨��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������̨�ٰ�����й�������д�������Ŀ�ܵ���ѧ���Ĺ㷺��ע��ij��ѧΪ���˽�ѧ���Թۿ����й�������д�������Ŀ��ϲ���̶ȣ��Ը�У����ѧ������������������飬�����Ƴ���ͼ��ʾ������ͳ��ͼ��������ͼ�У�������������ΪA�ࣨ�dz�ϲ������B�ࣨ��ϲ������C�ࣨһ�㣩��D�ࣨ��ϲ��������֪A���B����ռ�����ı���5��9����������ͳ��ͼ���ش��������⣺
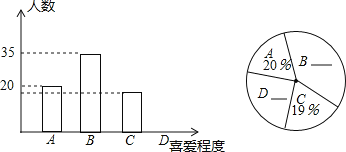
��1��д�����γ������������������
��2���벹ȫ����ͳ��ͼ��
��3������У��2000��ѧ����������ƹۿ����й�������д�������Ŀ��ϲ����ѧ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����ͼ����֪����ABC�У���BAC��40����BD��AC��D��CE��AB��E��BD��CE����ֱ�߽��ڵ�F������BFC�Ķ�����
��2���ڣ�1���Ļ����ϣ�����BACÿ������10�������ڱ仯��������ABC����ACBʼ�ձ�������ǣ�����t�루0��t��14��������BFC����BAC���������У���һ��Ϊ��һ��������ʱ����t��ֵ��
��3���ڣ�2���Ļ����ϣ���ABD����ACE�Ľ�ƽ���߽��ڵ�G����BGC�Ƿ�Ϊ��ֵ������ǣ���ֱ��д����BGC��ֵ��������ǣ���д����BGC����α仯�ģ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ȫ�ȵġ�ABC �͡�DBE ��ͼ 1 ��ʽ�ڷţ����С�ACB����DEB��90������A����D��30������ E ���� AB �ϣ�DE ����ֱ�߽� AC ����ֱ���ڵ� F��
��1������ͼ 1 �еġ�DBE �Ƶ� B ��˳ʱ�뷽����ת�������� 0��������60���������������䣬��ͼ 2������ֱ��д���߶� AF��EF��DE ��������ϵ��
��2������ͼ 1 �еġ�DBE �Ƶ� B ��˳ʱ�뷽����ת�������� 60��ܦ¡�180���������������䣮
����ͼ 3����1�����߶� AF��EF��DE ��������ϵ�Ƿ���Ȼ����������������֤���ý��ۣ�������������д���µĽ��۲�֤����
����ͼ 4��AB �е�Ϊ M��BE �е�Ϊ N���� BC�� 2![]() ������ MN�������� ��ʱ��MN ����������ֵΪ ������ ��ֱ��д���𰸼��ɣ�
������ MN�������� ��ʱ��MN ����������ֵΪ ������ ��ֱ��д���𰸼��ɣ�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com