
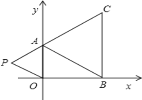
【题目】如图,在下面直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a、b、c满足关系式![]() .
.
(1)求a、b、c的值;
(2)如果在第二象限内有一点P(m,![]() ),请用含m的式子表示四边形ABOP的面积;
),请用含m的式子表示四边形ABOP的面积;
(3)在(2)的条件下,是否存在点P,使四边形ABOP的面积与△ABC的面积相等?若存在,求出点P的坐标,若不存在,请说明理由.
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)
;(2)![]() ;(3)存在,点P(
;(3)存在,点P(![]() ,
,![]() ).
).
【解析】
(1)根据二次根式、绝对值、平方的非负性可得结论;
(2)根据P和A、B的坐标,由S四边形ABOP=S△AOP+S△AOB可得结论;
(3)根据四边形ABOP的面积与△ABC的面积相等,列式可得m=-3,从而得P的坐标.
解:(1)∵![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ;
;
(2)由(1)知:OA=2,OB=3,点P(m,![]() ),
),
∴S四边形ABOP=S△AOP+S△AOB=![]() AO|xP|+
AO|xP|+![]() AOOB=
AOOB=![]() ×2×3=
×2×3=![]() ;
;
(3)∵B(3,0),C(3,4),
∴BC⊥x轴,
∴S△ABC=![]() BCxB=
BCxB=![]() ×4×3=6,
×4×3=6,
∴![]() =6,
=6,
∴![]() ,
,
则当![]() 时,四边形ABOP的面积与△ABC的面积相等,此时P(
时,四边形ABOP的面积与△ABC的面积相等,此时P(![]() ,
,![]() ).
).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某汽车专卖店销售A、B两种型号的新能源汽车,上周售出1辆A型车和3辆B型车,销售额为96万元;本周已售出2辆A型车和1辆B型车,销售额为62万元
(1). 求每辆A型车和B型车的售价各为多少万元?
(2). 甲公司拟向该店购买A、B两种型号的新能源汽车共8辆,购车费不少于165万元,且不超过190万元,则有哪几种购车方案?几种购车方案中所需购车费最少是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E为CD上一点,连接AE、BD,且AE、BD交于点F,S△DEF:S△ABF=4:25,则DE:EC=( )
A.2:5
B.2:3
C.3:5
D.3:2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=kx+6分别与x轴、y轴交于点E,F,已知点E的坐标为(﹣8,0),点A的坐标为(﹣6,0).
(1)求k的值;
(2)若点P(x,y)是该直线上的一个动点,且在第二象限内运动,试写出△OPA的面积S关于x的函数解析式,并写出自变量x的取值范围.
(3)探究:当点P运动到什么位置时,△OPA的面积为![]() ,并说明理由.
,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
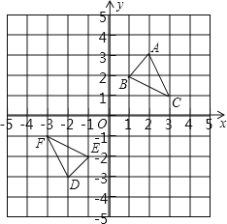
【题目】如图,△DEF是△ABC经过某种变换得到的图形,点A与点D,点![]() 与点E,点
与点E,点![]() 与点F分别是对应点,观察点与点的坐标之间的关系,解答下列问题:
与点F分别是对应点,观察点与点的坐标之间的关系,解答下列问题:
(1)分别写出点A与点D,点![]() 与点E,点
与点E,点![]() 与点F的坐标,并说说对应点的坐标有哪些特征;
与点F的坐标,并说说对应点的坐标有哪些特征;
(2)若点![]() 与点
与点![]() 也是通过上述变换得到的对应点,求
也是通过上述变换得到的对应点,求![]() 、b的值
、b的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,矩形![]() 的顶点
的顶点![]() 、
、![]() 分别在
分别在![]() 轴与
轴与![]() 轴上,且点
轴上,且点![]() ,点
,点![]() ,点
,点![]() 为矩形
为矩形![]() 、
、![]() 两边上的一个点.
两边上的一个点.

(1)当点![]() 与
与![]() 重合时,求直线
重合时,求直线![]() 的函数解析式;
的函数解析式;
(2)如图②,当![]() 在
在![]() 边上,将矩形沿着
边上,将矩形沿着![]() 折叠,点
折叠,点![]() 对应点
对应点![]() 恰落在
恰落在![]() 边上,求此时点
边上,求此时点![]() 的坐标.
的坐标.
(3)是否存![]() 在使
在使![]() 为等腰三角形?若存在,直接写出点
为等腰三角形?若存在,直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里装有黑、白两种颜色的球共50个,这些球除颜色外其余完全相同.王颖做摸球试验,搅匀后,她从盒子里随机摸出一个球记下颜色后,再把球放回盒子中,不断重复上述过程,下表是试验中的一组统计数据:
摸球的次数 | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
摸到白球的次数 | 65 | 124 | 178 | 302 | 480 | 601 | 1800 |
摸到白球的频率 |
|
|
|
|
|
|
|
(1)若从盒子里随机摸出一个球,则摸到白球的概率的估计值为______.
(2)试估算盒子里黑、白两种颜色的球各有多少个?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com