
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:解答题
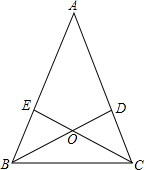 如图,在△ABC中,AB=AC,分别根据以下条件,说明△OBC是等腰三角形.
如图,在△ABC中,AB=AC,分别根据以下条件,说明△OBC是等腰三角形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示为在场地上画平行线的简单方法,将皮带尺从P拉到A,取AP的中点M,并且在点M上竖一木桩,再将皮带从n上的另一点B拉向M,使它过M,取MC=BM,那么过P、C两点的直线m就是平行于n的一条直线,为什么?
如图所示为在场地上画平行线的简单方法,将皮带尺从P拉到A,取AP的中点M,并且在点M上竖一木桩,再将皮带从n上的另一点B拉向M,使它过M,取MC=BM,那么过P、C两点的直线m就是平行于n的一条直线,为什么?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
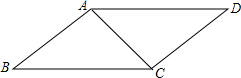 如图,已知平行四边形ABCD中,AB=40cm,AC=30cm,BC=50cm,有一动点P从点B出发,以1cm/秒的速度沿B→C→D运动至D点停止,当运动时间为20或25或14或80秒时,以P,A,C为顶点的三角形是等腰三角形.
如图,已知平行四边形ABCD中,AB=40cm,AC=30cm,BC=50cm,有一动点P从点B出发,以1cm/秒的速度沿B→C→D运动至D点停止,当运动时间为20或25或14或80秒时,以P,A,C为顶点的三角形是等腰三角形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com