
分析 (1)等式左边随序号在变化的只有第二个因数,并且是每个等式的序号数;等式右边第一个幂的底数,它是序号的3倍加1,第二个幂的底数显然也是序号数.
(2)将左边第二个因数用n表示,那么右边第一个底数是(3n+1),第二个底数为n,可完整表示出第n个等式.
解答 解:(1)等式左边随序号在变化的只有第二个因数,并且是每个等式的序号数;
等式右边第一个幂的底数,它是序号的3倍加1,第二个幂的底数显然也是序号数.
所以第4个等式为:1+6×4=(3×4+1)2-9×42,
即1+6×4=132-9×42;
答案为:4,13,4.
(2)第n个等式为:1+6n=(3n+1)2-9n2;
∵右边=(3n)2+2•(3n)•1+1-9n2
=9n2+6n+1-9n2
=6n+1=左边
∴1+6n=(3n+1)2-9n2成立.
点评 通过观察,分析、归纳并发现其中的规律,并应用发现的规律解决问题是应该具备的基本能力.本题的关键是看清没个等式在变化的数与等式序号间的关系.


 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案科目:初中数学 来源: 题型:选择题
| A. | m$<\frac{1}{2}$ | B. | m$>\frac{1}{2}$ | C. | m$>-\frac{1}{2}$ | D. | m$<-\frac{1}{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
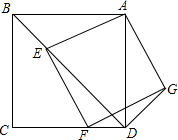 如图,已知正方形ABCD中,点E是对角线BD上一点,连接AE,以AE为边作正方形AEF0,使得点F在CD边上,连接DG,
如图,已知正方形ABCD中,点E是对角线BD上一点,连接AE,以AE为边作正方形AEF0,使得点F在CD边上,连接DG,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com