
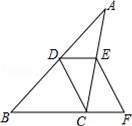
如图,在△ABC中,D、E分别是边AB、AC的中点,延长BC至点F,使得CF=
 BC,连结CD、DE、EF.
BC,连结CD、DE、EF.
(1)求证:四边形CDEF是平行四边形.
(2)若四边形CDEF的面积为8,则△ABC的面积为 8 .

【考点】平行四边形的判定与性质.
【分析】(1)欲证明四边形CDEF是平行四边形,只需推知DE∥CF,DE=CF;
(2)在四边形CDEF与△ABC中,CF=
 BC,且它们的高相等.
BC,且它们的高相等.
【解答】(1)证明:∵如图,在△ABC中,D、E分别是边AB、AC的中点,
∴DE∥BC且DE=
 BC.
BC.
又∵CF=
 BC,
BC,
∴DE=CF,
∴四边形CDEF是平行四边形.
(2)解:∵DE∥BC,
∴四边形CDEF与△ABC的高相等,设为h,
又∵CF=
 BC,
BC,
∴S△ABC=
 BC•h=CF•h=8,
BC•h=CF•h=8,
故答案是:8.


【点评】本题考查了平行四边形的判定与性质.平行四边形的判定方法共有五种,应用时要认真领会它们之间的联系与区别,同时要根据条件合理、灵活地选择方法.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
某汽车制造厂开发了一种新式电动汽车,计划一年生成安装
240辆.由于抽调不出足够的熟练工来完成这种新式电动汽车的安装,工厂决定
招聘 一些新工人,他们经过培训后上岗,也能独立进行电动汽车的安装.生产
开始后,调研部门发现:1名熟练工和2名新工人每月可安装8辆电动汽车;
2名熟练工和3名新工人每月可安装14辆电动汽车.
(1)每名熟练工和每名新工人每月分别可安装多少辆电动汽车?
(2)设工厂招聘n(0<n<10)名新工人,为使招聘的新工人和抽调的熟练工刚好能完成一年的安装任务,那么工厂有哪些招聘方案?
(3)在(2)的条件下,工厂给每名熟练工每月发2000元的工资,给每名新工
人每月发1200元的工资,要求新工人的数量多于熟练工,为使工厂每月支
出的工资总额W(元)尽可能少,工厂应招聘多少名新工人?
查看答案和解析>>
科目:初中数学 来源: 题型:
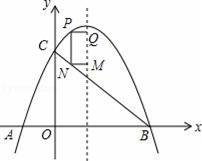
如图,平面直角坐标系中,抛物线y=ax2+bx+2与x轴分别交于点A(﹣1,0)、B(3,0),与y轴交于点C,连结BC.点P是BC上方抛物线上一点,过点P作y轴的平行线,交BC于点N,分别过P、N两点作x轴的平行线,交抛物线的对称轴于点Q、M,设P点的横坐标为m.
(1)求抛物线所对应的函数关系式.
(2)当点P在抛物线对称轴左侧时,求四边形PQMN周长的最大值.
(3)当四边形PQMN为正方形时,求m的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com