
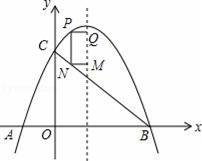
如图,平面直角坐标系中,抛物线y=ax2+bx+2与x轴分别交于点A(﹣1,0)、B(3,0),与y轴交于点C,连结BC.点P是BC上方抛物线上一点,过点P作y轴的平行线,交BC于点N,分别过P、N两点作x轴的平行线,交抛物线的对称轴于点Q、M,设P点的横坐标为m.
(1)求抛物线所对应的函数关系式.
(2)当点P在抛物线对称轴左侧时,求四边形PQMN周长的最大值.
(3)当四边形PQMN为正方形时,求m的值.

【考点】二次函数综合题.
【分析】(1)设交点式y=a(x+1)(x﹣3),然后把C点坐标代入求出a即可得到抛物线的解析式;
(2)先利用对称轴确定抛物线的对称轴方程,再利用待定系数法求出直线BC的解析式,接着利用m表示出PN和PQ,从而得到四边形PQMN周长与m的二次函数关系,然后利用二次函数的性质求四边形PQMN周长的最大值;
(3)分类讨论:当0<m<1时,利用PQ=PN得到﹣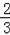
 m2+2m=1﹣m;当1<m<3时,利用PQ=PN得到﹣
m2+2m=1﹣m;当1<m<3时,利用PQ=PN得到﹣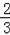
 m2+2m=m﹣1,然后分别解一元二次方程得到满足条件的m的值.
m2+2m=m﹣1,然后分别解一元二次方程得到满足条件的m的值.
【解答】解:(1)当x=0时,y=ax2+bx+2=2,则C(0,2),
设抛物线解析式为y=a(x+1)(x﹣3),
把C(0,2)代入得a•1•(﹣3)=2,解得a=﹣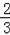
 ,
,
所以抛物线的解析式为y=﹣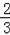
 (x+1)(x﹣3),即y=﹣
(x+1)(x﹣3),即y=﹣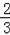
 x2+
x2+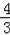
 x+2;
x+2;
(2)∵抛物线与x轴分别交于点A(﹣1,0)、B(3,0),
∴抛物线的对称轴为直线x=1,
设直线BC的解析式为y=px+q,
把C(0,2),B(3,0)代入得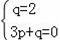
 ,解得
,解得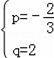
 ,
,
所以直线BC的解析式为y=﹣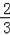
 x2+2,
x2+2,
设P(m,﹣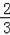
 m2+
m2+
 m+2),则N(m,﹣
m+2),则N(m,﹣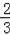
 m+2),
m+2),
∴PN=﹣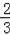
 m2+
m2+
 m+2﹣(﹣
m+2﹣(﹣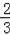
 m+2)=﹣
m+2)=﹣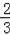
 m2+2m,
m2+2m,
而PQ=1﹣m,
∴四边形PQMN周长=2(﹣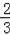
 m2+2m+1﹣m)=﹣
m2+2m+1﹣m)=﹣
 m2+2m+2=﹣
m2+2m+2=﹣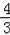
 (m﹣
(m﹣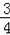
 )2+
)2+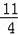
 (0<m<1),
(0<m<1),
∴当m=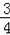
 时,四边形PQMN周长有最大值,最大值为
时,四边形PQMN周长有最大值,最大值为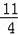
 ;
;
(3)当0<m<1时,PQ=1﹣m,
若PQ=PN时,四边形PQMN为正方形,即﹣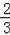
 m2+2m=1﹣m,
m2+2m=1﹣m,
整理得2m2﹣9m+3=0,解得m1=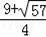
 (舍去),m2=
(舍去),m2=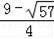
 ,
,
当1<m<3时,PQ=m﹣1,
若PQ=PN时,四边形PQMN为正方形,即﹣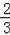
 m2+2m=m﹣1,
m2+2m=m﹣1,
整理得2m2﹣3m﹣3=0,解得m1=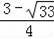
 (舍去),m2=
(舍去),m2=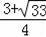
 ,
,
综上所述,当m=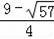
 或m=
或m=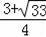
 时,四边形PQMN为正方形.
时,四边形PQMN为正方形.
【点评】本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征、二次函数的性质和正方形的性质;会利用待定系数法求函数解析式;理解坐标与图形性质;会解一元二次方程.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:
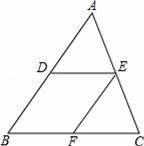
如图,在△ABC中,D、E分别是AB、AC的中点,过点E作EF∥AB,交BC于点F.
(1)求证:四边形DBFE是平行四边形;
(2)当△ABC满足什么条件时,四边形DBFE是菱形?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
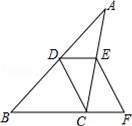
如图,在△ABC中,D、E分别是边AB、AC的中点,延长BC至点F,使得CF=
 BC,连结CD、DE、EF.
BC,连结CD、DE、EF.
(1)求证:四边形CDEF是平行四边形.
(2)若四边形CDEF的面积为8,则△ABC的面积为 8 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com