
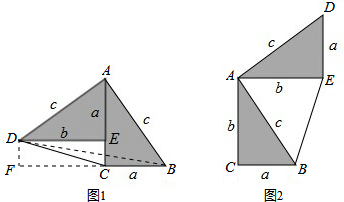
分析 首先连结BD,过点B作DE边上的高BF,则BF=b-a,两种方法表示出S五边形ACBED,两者相等,整理即可得证.
解答 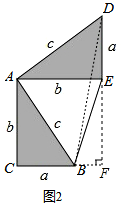 证明:如图2,连结BD,过点B作DE边上的高BF
证明:如图2,连结BD,过点B作DE边上的高BF
∵S五边形ACBED=S△ACB+S△ABE+S△ADE=$\frac{1}{2}$ab+$\frac{1}{2}$b2+$\frac{1}{2}$ab
又∵S五边形ACBED=S△ACB+S△ABD+S△BDE=$\frac{1}{2}$ab+$\frac{1}{2}$c2+$\frac{1}{2}$a(b-a)
∴$\frac{1}{2}$ab+$\frac{1}{2}$b2+$\frac{1}{2}$ab=$\frac{1}{2}$ab+$\frac{1}{2}$c2+$\frac{1}{2}$a(b-a)
∴a2+b2=c2.
故答案为:BD,过点B作DE边上的高BF,S△ACB+S△ABE+S△ADE=$\frac{1}{2}$ab+$\frac{1}{2}$b2+$\frac{1}{2}$ab,S△ACB+S△ABD+S△BDE=$\frac{1}{2}$ab+$\frac{1}{2}$c2+$\frac{1}{2}$a(b-a),$\frac{1}{2}$ab+$\frac{1}{2}$b2+$\frac{1}{2}$ab=$\frac{1}{2}$ab+$\frac{1}{2}$c2+$\frac{1}{2}$a(b-a).
点评 此题考查了勾股定理的证明,用两种方法表示出五边形ACBED的面积是解本题的关键.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:解答题
 快、慢两车分别从相距480千米路程的甲、乙两地同时出发,匀速行驶,先相向而行,途中慢车因故停留1小时,然后以原速度继续向甲地行驶,到达甲地后停止行驶;快车达到乙地后,立即按原路原速返回甲地(快车掉头的时间忽略不计),快、慢两车距乙地的路程y(千米)与所用时间x(小时)之间的函数图象如图.请结合图象信息解答下列问题:
快、慢两车分别从相距480千米路程的甲、乙两地同时出发,匀速行驶,先相向而行,途中慢车因故停留1小时,然后以原速度继续向甲地行驶,到达甲地后停止行驶;快车达到乙地后,立即按原路原速返回甲地(快车掉头的时间忽略不计),快、慢两车距乙地的路程y(千米)与所用时间x(小时)之间的函数图象如图.请结合图象信息解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
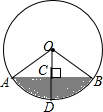 将一盛有不足半杯水的圆柱形玻璃水杯拧紧杯盖后放倒,水平放置在桌面上,水杯的底面如图所示,已知水杯的半径是4cm,水面宽度AB是4$\sqrt{3}$cm.
将一盛有不足半杯水的圆柱形玻璃水杯拧紧杯盖后放倒,水平放置在桌面上,水杯的底面如图所示,已知水杯的半径是4cm,水面宽度AB是4$\sqrt{3}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
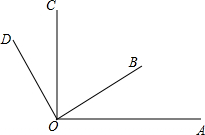 如图,已知∠AOC与∠BOD都是直角,∠BOC=59°.
如图,已知∠AOC与∠BOD都是直角,∠BOC=59°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com