
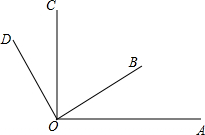
 如图,已知∠AOC与∠BOD都是直角,∠BOC=59°.
如图,已知∠AOC与∠BOD都是直角,∠BOC=59°.分析 (1)根据∠AOB+∠BOC=90°和∠DOC+∠BOC=90°即可解题;
(2)把3个角的度数相加可得出∠AOD的度数;
(3)根据∠AOB与∠DOC的度数大小即可求得∠AOB与∠DOC的大小关系;
(4)根据等角的余角相等,可得(3)的关系依然成立.
解答 解:(1)∵∠AOB+∠BOC=90°,
∴∠COD=90°-59°=31°,
∵∠DOC+∠BOC=90°,
∴∠AOB=90°-59°=31°;
(2)∠AOD=∠AOB+∠BOC+∠DOC=121°.
(3)∵∠AOB=31°,∠DOC=31°,
∴∠AOB=∠DOC;
(4)成立;
∵∠AOB+∠BOC=90°,∠DOC+∠BOC=90°,
∴∠AOB=∠DOC.
点评 本题考查了余角和补角的知识,解答本题的关键是掌握:等角的余角相等.


 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
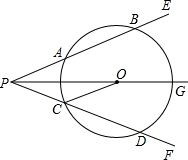 如图所示,射线PG平分∠EPF,O为射线PG上一点,以O为圆心,10为半径作⊙O,分别与∠EPF两边相交于A、B和C、D,连结OA,此时有OC∥PE
如图所示,射线PG平分∠EPF,O为射线PG上一点,以O为圆心,10为半径作⊙O,分别与∠EPF两边相交于A、B和C、D,连结OA,此时有OC∥PE查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com