
分析 实数的分类:$\left\{\begin{array}{l}{有理数\left\{\begin{array}{l}{正有理数}\\{0}\\{负有理数}\end{array}\right.}\\{无理数\left\{\begin{array}{l}{正无理数}\\{负无理数}\end{array}\right.}\end{array}\right.$,依此即可求解.
解答 解:(1)是有理数的有-13,0,2,-22,0.3;
(2)是无理数的有 π,$\sqrt{3}$,2.121121112…(两个2之间依次多一个1);
(3)是整数的有 13,0,2,-22;
(4)是分数的有 0.3.
故答案为:-13,0,2,-22,0.3;π,$\sqrt{3}$,2.121121112…(两个2之间依次多一个1);13,0,2,-22;0.3.
点评 本题主要考查了实数的定义,要求掌握实数的范围以及分类方法.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
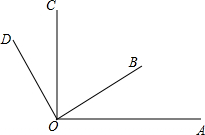 如图,已知∠AOC与∠BOD都是直角,∠BOC=59°.
如图,已知∠AOC与∠BOD都是直角,∠BOC=59°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com