
【题目】已知:关于x的方程kx2﹣(3k﹣1)x+2(k﹣1)=0
(1)求证:无论k为任何实数,方程总有实数根;
(2)若此方程有两个实数根x1,x2,且|x1﹣x2|=2,求k的值.
【答案】(1)证明详见解析;(2) 1或![]() .
.
【解析】试题分析:(1)确定判别式的范围即可得出结论;
(2)根据根与系数的关系表示出x1+x2,x1x2,继而根据题意得出方程,解出即可.
(1)证明:①当k=0时,方程是一元一次方程,有实数根;
②当k≠0时,方程是一元二次方程,
∵△=(3k﹣1)2﹣4k×2(k﹣1)=(k+1)2≥0,
∴无论k为任何实数,方程总有实数根.
(2)解:∵此方程有两个实数根x1,x2,
∴x1+x2=![]() ,x1x2=
,x1x2=![]() ,
,
∵|x1﹣x2|=2,
∴(x1﹣x2)2=4,
∴(x1+x2)2﹣4x1x2=4,即![]() ﹣4×
﹣4×![]() =4,
=4,
解得:![]() =±2,
=±2,
即k=1或k=﹣,
经检验k=1或k=﹣是方程的解,
则k=1或k=﹣.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源: 题型:
【题目】如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用![]() ,
,![]() 表示直角三角形的两直角边(
表示直角三角形的两直角边(![]() ),下列四个说法:
),下列四个说法:

①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() .
.
其中说法正确的是 …………………………………………………………( )
A. ①② B. ①②③ C. ①②④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料并解决有关问题:
我们知道,|m|= .现在我们可以用这一结论来化简含有绝对值的代
.现在我们可以用这一结论来化简含有绝对值的代
数式,如化简代数式|m+1|+|m﹣2|时,可令 m+1=0 和 m﹣2=0,分别求得 m=﹣1,m=2(称﹣1,2 分别为|m+1|与|m﹣2|的零点值).在实数范围内, 零点值 m=﹣1 和 m=2 可将全体实数分成不重复且不遗漏的如下 3 种情况:
(1)m<﹣1;(2)﹣1≤m<2;(3)m≥2.从而化简代数式|m+1|+|m﹣2| 可分以下 3 种情况:
(1)当 m<﹣1 时,原式=﹣(m+1)﹣(m﹣2)=﹣2m+1;
(2)当﹣1≤m<2 时,原式=m+1﹣(m﹣2)=3;
(3)当 m≥2 时,原式=m+1+m﹣2=2m﹣1.
综上讨论,原式=
通过以上阅读,请你解决以下问题:
(1)分别求出|x﹣5|和|x﹣4|的零点值;
(2)化简代数式|x﹣5|+|x﹣4|;
(3)求代数式|x﹣5|+|x﹣4|的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.

(1)求证:△AEC≌△BED;
(2)若∠1=42°,求∠BDE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题:①若![]() ,则
,则![]() ;②直角三角形的两个锐角互余:③如果
;②直角三角形的两个锐角互余:③如果![]() ,那么
,那么![]() ④
④![]() 个角都是直角的四边形是正方形.其中,原命题和逆命题均为真命题的有( )
个角都是直角的四边形是正方形.其中,原命题和逆命题均为真命题的有( )
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电脑经销商计划购进一批电脑机箱和液晶显示器,若购电脑机箱10台和液液晶显示器8台,共需要资金7000元;若购进电脑机箱2台和液示器5台,共需要资金4120元.
(1)每台电脑机箱、液晶显示器的进价各是多少元?
(2)该经销商购进这两种商品共50台,而可用于购买这两种商品的资金不超过22240元.根据市场行情,销售电脑机箱、液晶显示器一台分别可获利10元和160元.该经销商希望销售完这两种商品,所获利润不少于4100元.试问:该经销商有哪几种进货方案?哪种方案获利最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将Rt△ABC沿某条直线折叠,使斜边的两个端点A与B重合,折痕为DE.

(1)如果AC=6cm,BC=8cm,试求△ACD的周长;
(2)如果∠CAD:∠BAD=1:2,求∠B的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
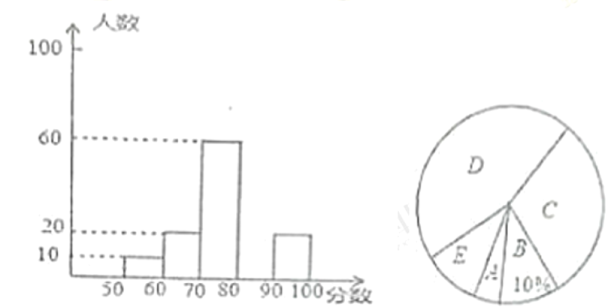
【题目】七年级数学研究学习小组在某↑字路口随机调查部分市民对“社会主义核心价值观”的了解情况,统计结果后绘制了如图的两副不完整的统计图,请结合图中相关数据回答下列问题:
得分 | |
|
|
|
|
|
|
|
|
|
|
(1)本次调查的总人数为 人, 在扇形统计图中“心所在扇形的圆心角的度数为 :
(2)补全频数分布图:
(3)若在这周里,该路口共有![]() 人通过,请估计得分超过
人通过,请估计得分超过![]() 的约有多少人?
的约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的曲线是函数y=![]() (m为常数)图象的一支.
(m为常数)图象的一支.
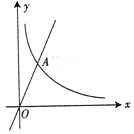
(1)求常数m的取值范围;
(2)若该函数的图象与正比例函数y=2x的图象在第一象限的交点为A(2,n),求点A的坐标及反比例
函数的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com