
【题目】在正五边形的外接圆中,任一边所对的圆周角的度数为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 或
或![]()
【答案】D
【解析】
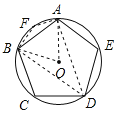
画出图形,连接OA、OB、BD、AD,在弧AB上取点F,连接AF、BF,由正五边形的性质得出AB=BC=CD=DE=AE,∠AOB=72°,由圆周角定理得出∠ADB=![]() ∠AOB=36°,由圆内接四边形的性质得出∠AFB=180°-∠ADB=144°,即可得出结论.
∠AOB=36°,由圆内接四边形的性质得出∠AFB=180°-∠ADB=144°,即可得出结论.
解:连接OA、OB、BD、AD,在弧AB上取点F,连接AF、BF,
如图所示:
∵五边形ABCDE是正五边形,
∴AB=BC=CD=DE=AE,∠AOB=360°÷5=72°,
∴∠ADB=![]() ∠AOB=36°,
∠AOB=36°,
∴∠AFB=180°-∠ADB=144°,
即在正五边形的外接圆中,任一边所对的圆周角的度数为36°或144°;
故选:D.


科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.为了解全国中学生视力的情况,应采用普查的方式
B.某种彩票中奖的概率是![]() ,买1000张这种彩票一定会中奖
,买1000张这种彩票一定会中奖
C.从2000名学生中随机抽取200名学生进行调查,样本容量为200名学生
D.从只装有白球和绿球的袋中任意摸出一个球,摸出黑球是确定事件
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知抛物线![]() 与x轴相交于A、B两点(A左B右),与y轴交于点C.其顶点为D.
与x轴相交于A、B两点(A左B右),与y轴交于点C.其顶点为D.
(1)求点D的坐标和直线BC对应的一次函数关系式;
(2)若正方形PQMN的一边PQ在线段AB上,另两个顶点M、N分别在BC、AC上,试求M、N两点的坐标;
(3)如图1,E是线段BC上的动点,过点E作DE的垂线交BD于点F,求DF的最小值.
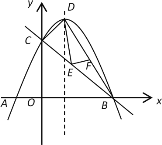
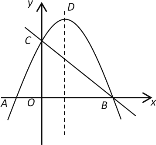
(图1) (图2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形ABCD的顶点A点,D点分别在x轴、y轴上,对角线BD∥x轴,反比例函数![]() 的图象经过矩形对角线的交点E,若点A(2,0),D(0,4),则k的值为( )
的图象经过矩形对角线的交点E,若点A(2,0),D(0,4),则k的值为( )
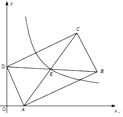
A.16B.20C.32D.40
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=10,BC=12,点D是BC上一点,DE∥AC,DF∥AB,则△BED与△DFC的周长的和为( )
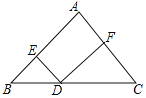
A. 34B. 32C. 22D. 20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】依托独特的气候资源,天然肥沃的优质土壤,广元市大力推广蔬菜种植,疫情防控期间,某蔬菜种植基地通过电商平台将蔬菜销往全国各地,销量大幅度提升.该基地为提高蔬菜产量,计划对甲、乙两种型号蔬菜大棚进行改造,根据预算,改造2个甲种型号大棚比1个乙种型号大棚多需资金6万元,改造1个甲种型号大棚和2个乙种型号大棚共需资金48万元.
(1)求改造1个甲种型号和1个乙种型号大棚所需资金分别是多少万元;
(2)已知改造1个甲种型号大棚需要5天,改造1个乙种型号大棚需要3天,该基地计划用126万元资金改造一定数量的两种型号蔬菜大棚,且要求改造时间总共不超过50天,请问:有几种改造方案?哪种方案改造时间最短?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在矩形![]() 中,
中,![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() 上的点,过点
上的点,过点![]() 作
作![]() 的垂线交
的垂线交![]() 于点
于点![]() ,以
,以![]() 为直径作半圆
为直径作半圆![]() .
.
(1)填空:点![]() _____________(填“在”或“不在”)
_____________(填“在”或“不在”)![]() 上;当
上;当![]() 时,
时,![]() 的值是_____________;
的值是_____________;
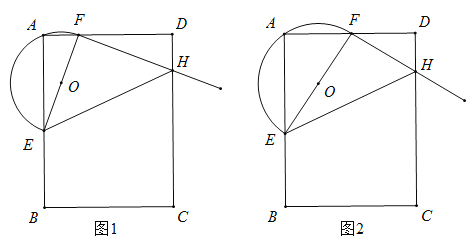
(2)如图1,在![]() 中,当
中,当![]() 时,求证:
时,求证:![]() ;
;
(3)如图2,当![]() 的顶点
的顶点![]() 是边
是边![]() 的中点时,请直接写出
的中点时,请直接写出![]() 三条线段的数量关系.
三条线段的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,AB=AC.

(1)试用直尺和圆规在AC上找一点D,使AD=BD(不写作法,但需保留作图痕迹).
(2)在(1)中,连接BD,若BD=BC,求∠A的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,在三角形纸片ABC中,∠BAC=78°,AC=10.数学实践课上,小敏用5张这样的三角形纸片拼成了一个内外都是正五边形的图形(如图2所示),并通过上网查到以下几个数据:sin78°≈0.98,cos78°≈0.21,tan78°≈4.7.请你帮助她解决下列问题:

(1)∠ABC= °;
(2)求正五边形GHMNC的边GC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com