
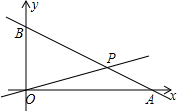
 在如图所示的直角坐标系中,O为原点,直线y=-$\frac{1}{2}$x+8与x轴、y轴分别交于A、B两点,设直线OP与线段AB相交于P点,且$\frac{{S}_{△AOP}}{{S}_{△BOP}}$=$\frac{1}{3}$,试求点P的坐标.
在如图所示的直角坐标系中,O为原点,直线y=-$\frac{1}{2}$x+8与x轴、y轴分别交于A、B两点,设直线OP与线段AB相交于P点,且$\frac{{S}_{△AOP}}{{S}_{△BOP}}$=$\frac{1}{3}$,试求点P的坐标. 分析 根据一次函数解析式求出OA、OB,然后求出$\frac{AP}{AB}$,过点P作PC⊥OA于C,得到PC∥BO,求出△PCA与△BOA相似,根据相似三角形对应边成比例列式求出PC、AC,再求出OC,然后写出点P的坐标即可.
解答 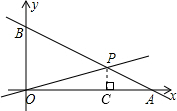 解:令x=0得,y=8,则B的坐标为(0,8),即BO=8,
解:令x=0得,y=8,则B的坐标为(0,8),即BO=8,
令y=0得,-$\frac{1}{2}$x+8=0,解得x=16,
则A的坐标为(16,0),即OA=16,
又∵$\frac{{S}_{△AOP}}{{S}_{△BOP}}$=$\frac{1}{3}$,
∴$\frac{AP}{BP}$=$\frac{1}{3}$,
∴$\frac{AP}{AB}$=$\frac{1}{4}$,
过点P作PC⊥OA于点C,则PC∥BO,
∴△PCA∽△BOA,
∴$\frac{AC}{AO}$=$\frac{PC}{BO}$=$\frac{AP}{AB}$,
∴PC=2,AC=4,
∴OC=OA-AC=12,
∴P的坐标为(12,2).
点评 本题考查了相似三角形的判定与性质,一次函数图象上点的坐标特征,难点在于根据等高的三角形的面积的比等于底边的比求出$\frac{AP}{BP}$,作辅助线构造出相似三角形是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,点A在反比例函数y=$\frac{4}{x}$的图象上,点B在反比例函数y=$\frac{k}{x}$(k<0)的图象上,且∠AOB=90°,tan∠OAB=$\frac{4}{3}$,则k的值是-$\frac{16}{9}$.
如图,点A在反比例函数y=$\frac{4}{x}$的图象上,点B在反比例函数y=$\frac{k}{x}$(k<0)的图象上,且∠AOB=90°,tan∠OAB=$\frac{4}{3}$,则k的值是-$\frac{16}{9}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
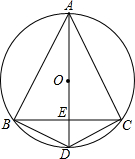 如图,△ABC是⊙O的内接等腰三角形,其顶角的平分线AD交⊙O于D,交BC于E,连接BD,DC.
如图,△ABC是⊙O的内接等腰三角形,其顶角的平分线AD交⊙O于D,交BC于E,连接BD,DC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
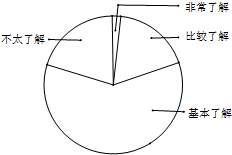 玉环县某学校数学兴趣小组在本校学生中开展主题为“五水共治”的专题调查活动,采取随机抽样的方法进行问卷调查.问卷调查的结果划分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级,划分等级后的数据整理如表:
玉环县某学校数学兴趣小组在本校学生中开展主题为“五水共治”的专题调查活动,采取随机抽样的方法进行问卷调查.问卷调查的结果划分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级,划分等级后的数据整理如表:| 等级 | 非常了解 | 比较了解 | 基本了解 | 不太了解 |
| 频数 | 4 | 36 | 120 | 40 |
| 频率 | 0.02 | 0.18 | m | 0.2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1.2×103米 | B. | 12×103米 | C. | 1.2×104米 | D. | 1.2×105米 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com