
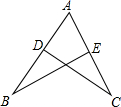
 如图,AB=AC,若要使△ABE≌△ACD,则添加的一个条件不能是( )
如图,AB=AC,若要使△ABE≌△ACD,则添加的一个条件不能是( )| A. | ∠B=∠C | B. | BE=CD | C. | BD=CE | D. | ∠ADC=∠AEB |
分析 已知条件AB=AC,还有公共角∠A,然后再结合选项所给条件和全等三角形的判定定理进行分析即可.
解答 解:A、添加∠B=∠C可利用ASA定理判定△ABE≌△ACD,故此选项不合题意;
B、添加BE=CD不能判定△ABE≌△ACD,故此选项符合题意;
C、添加BD=CE可得AD=AE,可利用利用SAS定理判定△ABE≌△ACD,故此选项不合题意;
D、添加∠ADC=∠AEB可利用AAS定理判定△ABE≌△ACD,故此选项不合题意;
故选:B.
点评 本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | -1 | C. | 1 | D. | 2 015 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 △ABC与△DEC的位置关系如图所示,其中E在BC上,AC交DE于F点,且AB∥DE.若△ABC与△DEC的面积相等,且EF=m,AB=n(n>m),则DF=$\frac{{n}^{2}-{m}^{2}}{m}$.
△ABC与△DEC的位置关系如图所示,其中E在BC上,AC交DE于F点,且AB∥DE.若△ABC与△DEC的面积相等,且EF=m,AB=n(n>m),则DF=$\frac{{n}^{2}-{m}^{2}}{m}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
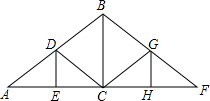 如图是屋架设计图的一部分,点D是斜梁AB的AB的中点,立柱BC、DE垂直于横梁AF.已知AB=12m,∠ADE=60°,则DE等于( )
如图是屋架设计图的一部分,点D是斜梁AB的AB的中点,立柱BC、DE垂直于横梁AF.已知AB=12m,∠ADE=60°,则DE等于( )| A. | 3m | B. | 2m | C. | 1m | D. | 4m |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
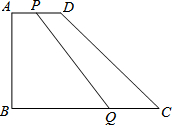 如图,在直角梯形ABCD中,∠B=90°,AD∥BC,且AD=4cm,AB=6cm,DC=10cm.若动点P从A点出发,以每秒4cm的速度沿线段AD、DC向C点运动;动点Q从C点出发以每秒5cm的速度沿CB向B点运动.当Q点到达B点时,动点P、Q同时停止运动.设点P、Q同时出发,并运动了t秒,
如图,在直角梯形ABCD中,∠B=90°,AD∥BC,且AD=4cm,AB=6cm,DC=10cm.若动点P从A点出发,以每秒4cm的速度沿线段AD、DC向C点运动;动点Q从C点出发以每秒5cm的速度沿CB向B点运动.当Q点到达B点时,动点P、Q同时停止运动.设点P、Q同时出发,并运动了t秒,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某商店销售甲、乙两种商品,现有如下信息:
某商店销售甲、乙两种商品,现有如下信息:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com