
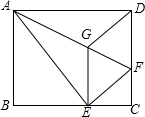
 如图,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG.给出以下结论:①DG=DF;②四边形EFDG是菱形;③EG2=$\frac{1}{2}$GF×AF;④当AG=6,EG=2$\sqrt{5}$时,BE的长为$\frac{12}{5}$$\sqrt{5}$,其中正确的结论个数是( )
如图,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG.给出以下结论:①DG=DF;②四边形EFDG是菱形;③EG2=$\frac{1}{2}$GF×AF;④当AG=6,EG=2$\sqrt{5}$时,BE的长为$\frac{12}{5}$$\sqrt{5}$,其中正确的结论个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 先依据翻折的性质和平行线的性质证明∠DGF=∠DFG,从而得到GD=DF,接下来依据翻折的性质可证明DG=GE=DF=EF,连接DE,交AF于点O.由菱形的性质可知GF⊥DE,OG=OF=$\frac{1}{2}$GF,接下来,证明△DOF∽△ADF,由相似三角形的性质可证明DF2=FO•AF,于是可得到GE、AF、FG的数量关系,过点G作GH⊥DC,垂足为H.利用(2)的结论可求得FG=4,然后再△ADF中依据勾股定理可求得AD的长,然后再证明△FGH∽△FAD,利用相似三角形的性质可求得GH的长,最后依据BE=AD-GH求解即可.
解答 解:∵GE∥DF,
∴∠EGF=∠DFG.
∵由翻折的性质可知:GD=GE,DF=EF,∠DGF=∠EGF,
∴∠DGF=∠DFG.
∴GD=DF.故①正确;
∴DG=GE=DF=EF.
∴四边形EFDG为菱形,故②正确;
如图1所示:连接DE,交AF于点O.
∵四边形EFDG为菱形,
∴GF⊥DE,OG=OF=$\frac{1}{2}$GF.
∵∠DOF=∠ADF=90°,∠OFD=∠DFA,
∴△DOF∽△ADF.
∴$\frac{DF}{AF}$=$\frac{OF}{DF}$,即DF2=FO•AF.
∵FO=$\frac{1}{2}$GF,DF=EG,
∴EG2=$\frac{1}{2}$GF•AF.故③正确;
如图2所示:过点G作GH⊥DC,垂足为H.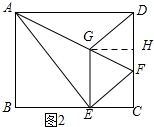
∵EG2=$\frac{1}{2}$GF•AF,AG=6,EG=2$\sqrt{5}$,
∴20=$\frac{1}{2}$FG(FG+6),整理得:FG2+6FG-40=0.
解得:FG=4,FG=-10(舍去).
∵DF=GE=2$\sqrt{5}$,AF=10,
∴AD=$\sqrt{A{F}^{2}-D{F}^{2}}$=4$\sqrt{5}$.
∵GH⊥DC,AD⊥DC,
∴GH∥AD.
∴△FGH∽△FAD.
∴$\frac{GH}{AD}$=$\frac{FG}{AF}$,即$\frac{GH}{4\sqrt{5}}$=$\frac{4}{10}$,
∴GH=$\frac{8\sqrt{5}}{5}$,
∴BE=AD-GH=4$\sqrt{5}$-$\frac{8\sqrt{5}}{5}$=$\frac{12\sqrt{5}}{5}$.故④正确.
故选D.
点评 本题主要考查的是四边形与三角形的综合应用,解答本题主要应用了矩形的性质、菱形的判定和性质、相似三角形的性质和判定、勾股定理的应用,利用相似三角形的性质得到DF2=FO•AF是解题答问题②的关键,依据相似三角形的性质求得GH的长是解答问题④的关键.


科目:初中数学 来源: 题型:解答题
 如图,已知AB是⊙O的直径,C是⊙O上一点,∠BAC的平分线交⊙O于点D,交⊙O的切线BE于点E,过点D作DF⊥AC,交AC的延长线于点F.
如图,已知AB是⊙O的直径,C是⊙O上一点,∠BAC的平分线交⊙O于点D,交⊙O的切线BE于点E,过点D作DF⊥AC,交AC的延长线于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
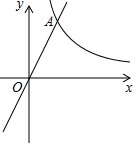 已知:如图,在平面直角坐标系xOy中,反比例函数y=$\frac{8}{x}$的图象与正比例函数y=kx(k≠0)的图象相交于横坐标为2的点A,平移直线OA,使它经过点B(3,0).
已知:如图,在平面直角坐标系xOy中,反比例函数y=$\frac{8}{x}$的图象与正比例函数y=kx(k≠0)的图象相交于横坐标为2的点A,平移直线OA,使它经过点B(3,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
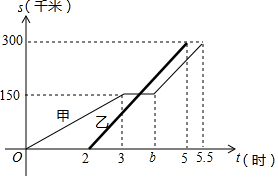 甲、乙两辆汽车沿同一路线从A地前往B地,甲以a千米/时的速度匀速行驶,途中出现故障后停车维修,修好后以2a千米/时的速度继续行驶;乙在甲出发2小时后匀速前往B地,设甲、乙两车与A地的路程为s(千米),甲车离开A地的时间为t(时),s与t之间的函数图象如图所示.
甲、乙两辆汽车沿同一路线从A地前往B地,甲以a千米/时的速度匀速行驶,途中出现故障后停车维修,修好后以2a千米/时的速度继续行驶;乙在甲出发2小时后匀速前往B地,设甲、乙两车与A地的路程为s(千米),甲车离开A地的时间为t(时),s与t之间的函数图象如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com