
【题目】如图,在平面直角坐标系中,二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 、
、![]() 两点,
两点,![]() 点在原点的左侧,
点在原点的左侧,![]() 点的坐标为
点的坐标为![]() ,与
,与![]() 轴交于
轴交于![]() 点,点
点,点![]() 是直线
是直线![]() 下方的抛物线上一动点.
下方的抛物线上一动点.
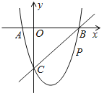
![]() 求这个二次函数的表达式.
求这个二次函数的表达式.
![]() 连接
连接![]() 、
、![]() ,并把
,并把![]() 沿
沿![]() 翻折,得到四边形
翻折,得到四边形![]() ,那么是否存在点
,那么是否存在点![]() ,使四边形
,使四边形![]() 为菱形?若存在,请求出此时点
为菱形?若存在,请求出此时点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
![]() 当点
当点![]() 运动到什么位置时,四边形
运动到什么位置时,四边形![]() 的面积最大?求出此时
的面积最大?求出此时![]() 点的坐标和四边形
点的坐标和四边形![]() 的最大面积.
的最大面积.
【答案】(1)![]() ;(2)
;(2)![]() 点的坐标为
点的坐标为![]() ;(3)
;(3)![]() 点的坐标为
点的坐标为![]() ,四边形
,四边形![]() 的面积的最大值为
的面积的最大值为![]() .
.
【解析】
(1)将B、C的坐标代入抛物线的解析式中即可求得待定系数的值;
(2)由于菱形的对角线互相垂直平分,若四边形POP′C为菱形,那么P点必在OC的垂直平分线上,据此可求出P点的纵坐标,代入抛物线的解析式中即可求出P点的坐标;
(3)由于△ABC的面积为定值,当四边形ABPC的面积最大时,△BPC的面积最大;过P作y轴的平行线,交直线BC于Q,交x轴于F,易求得直线BC的解析式,可设出P点的横坐标,然后根据抛物线和直线BC的解析式求出Q、P的纵坐标,即可得到PQ的长,以PQ为底,B点横坐标的绝对值为高即可求得△BPC的面积,由此可得到关于四边形ACPB的面积与P点横坐标的函数关系式,根据函数的性质即可求出四边形ABPC的最大面积及对应的P点坐标.
解:![]() 将
将![]() 、
、![]() 两点的坐标代入得
两点的坐标代入得![]() ,
,
解得:![]() ;
;
所以二次函数的表达式为:![]() ;
;
![]() 存在点
存在点![]() ,使四边形
,使四边形![]() 为菱形;
为菱形;
设![]() 点坐标为
点坐标为![]() ,
,![]() 交
交![]() 于
于![]()
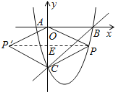
若四边形![]() 是菱形,则有
是菱形,则有![]() ;
;
连接![]() ,则
,则![]() 于
于![]() ,
,
∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]()
∴![]() ;
;
∴![]()
解得![]() ,
,![]() (不合题意,舍去),
(不合题意,舍去),
∴![]() 点的坐标为
点的坐标为![]()
![]() 过点
过点![]() 作
作![]() 轴的平行线与
轴的平行线与![]() 交于点
交于点![]() ,与
,与![]() 交于点
交于点![]() ,设
,设![]() ,
,
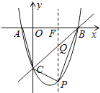
设直线![]() 的解析式为:
的解析式为:![]() ,
,
则![]() ,
,
解得:![]()
∴直线![]() 的解析式为
的解析式为![]() ,
,
则![]() 点的坐标为
点的坐标为![]() ;
;
当![]() ,
,
解得:![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
![]()
![]()
![]()
![]()
当![]() 时,四边形
时,四边形![]() 的面积最大
的面积最大
此时![]() 点的坐标为
点的坐标为![]() ,四边形
,四边形![]() 的面积的最大值为
的面积的最大值为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
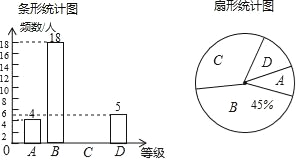
【题目】“足球运球”是中考体育必考项目之一.兰州市某学校为了解今年九年级学生足球运球的掌握情况,随机抽取部分九年级学生足球运球的测试成绩作为一个样本,按A,B,C,D四个等级进行统计,制成了如下不完整的统计图.(说明:A级:8分﹣10分,B级:7分﹣7.9分,C级:6分﹣6.9分,D级:1分﹣5.9分)
根据所给信息,解答以下问题:
(1)在扇形统计图中,C对应的扇形的圆心角是 度;
(2)补全条形统计图;
(3)所抽取学生的足球运球测试成绩的中位数会落在 等级;
(4)该校九年级有300名学生,请估计足球运球测试成绩达到A级的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用适当的方法解下列方程:
(1) x2﹣5x﹣6=0;
(2) (1﹣x)2﹣1=![]() ;
;
(3) 8x(x+2)=3x+6;
(4)(y+![]() )(y-
)(y-![]() )=20.
)=20.
查看答案和解析>>
科目:初中数学 来源: 题型:
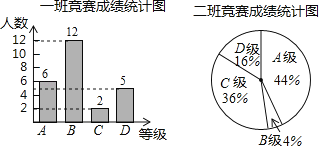
【题目】在学校组织的八年级数学竞赛中,每班参加比赛的人数相同,成绩分为A,B,C,D四个等级,其中相应等级的得分依次记为90分,80分,70分,60分,学校将八年级一班和二班的成绩整理并绘制成如下的统计图:
请你根据提供的信息解答下列问题:
(1)此次竞赛中二班80分以上(包括80分)的人数为 ;
(2)请你将表格补充完整:
平均数(分) | 中位数(分) | 众数(分) | |
一班 | 77.6 | 80 |
|
二班 | 77.6 |
| 90 |
(3)请从不同角度对这次竞赛成绩的结果进行分析.(至少两个角度)
查看答案和解析>>
科目:初中数学 来源: 题型:
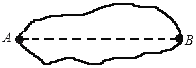
【题目】如图,要测量长春南溪湿地公园的荷花池A、B两端的距离,由于条件限制无法直接测得,请你用所学过的相似三角形的有关知识设计出一种测量方案.
具体要求:①用直尺或圆规画出测量的示意图,并说明应用的数学原理;②需要测量那些有关的数据;③待测量的数据可以用a、b、c、d等字母表示,最后表达出AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了创建书香校远,计划进一批图书,经了解.文学书的单价比科普书的单价少20元,用800元购进的文学书本数与用1200元购进的科普书本数相等.
(1)文学书和科普书的单价分别是多少元?
(2)该校计划用不超过5000元的费用购进一批文学书和科普书,问购进60本文学书后最多还能购进多少本科普书?
查看答案和解析>>
科目:初中数学 来源: 题型:
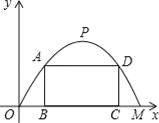
【题目】施工队要修建一个横断面为抛物线的公路隧道,其高度为6米,宽度OM为12米,现在O点为原点,OM所在直线为x轴建立直角坐标系(如图所示).
(1)直接写出点M及抛物线顶点P的坐标;
(2)求出这条抛物线的函数解析式;
(3)施工队计划在隧道门口搭建一个矩形“脚手架”ABCD,使A、D点在抛物线上,B、C点在地面OM上.为了筹备材料,需求出“脚手架”三根木杆AB、AD、DC的长度之和的最大值是多少?请你帮施工队计算一下.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com