
【题目】如图,在△ABC中,点O是边上一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交△BCA的外角平分线于点F. 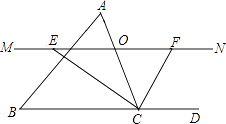
(1)探究OE与OF的数量关系并加以证明;
(2)当点O在边AC运动时,四边形BCFE会是菱形吗?若是,请加以证明;若不是,则说明理由.
(3)当点O在AC运动到什么位置,四边形AECF是矩形,请说明理由;
(4)在(3)问的基础上,△ABC满足什么条件时,四边形AECF是正方形?为什么?
【答案】
(1)解:OE=OF,
理由:∵MN∥BC,
∴∠OEC=∠BCE,∠OFC=∠DCF,
又∵CE平分∠BCO,CF平分∠DCO,
∴∠OCE=∠BCE,∠OCF=∠DCF,
∴∠OCE=∠OEC,∠OCF=∠OFC,
∴EO=CO,FO=CO,
∴OE=OF
(2)解:不可能.
如图所示,
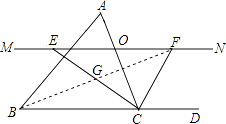
连接BF,
∵CE平分∠ACB,CF平分∠ACD,
∴∠ECF= ![]() ∠ACB+
∠ACB+ ![]() ∠ACD=
∠ACD= ![]() (∠ACB+∠ACD)=90°,
(∠ACB+∠ACD)=90°,
若四边形BCFE是菱形,则BF⊥EC,
但在△GFC中,不可能存在两个角为90°,所以不存在其为菱形
(3)解:当点O运动到AC的中点时,四边形AECF是矩形.
理由如下:
∵当点O运动到AC的中点时,AO=CO,
又∵EO=FO,
∴四边形AECF是平行四边形,
∵FO=CO,
∴AO=CO=EO=FO,
∴AO+CO=EO+FO,即AC=EF,
∴四边形AECF是矩形
(4)解:当点O运动到AC的中点时,且△ABC满足∠ACB为直角的直角三角形时,四边形AECF是正方形.
∵由(3)知,当点O运动到AC的中点时,四边形AECF是矩形,
已知MN∥BC,当∠ACB=90°,则
∠AOF=∠COE=∠COF=∠AOE=90°,
∴AC⊥EF,
∴四边形AECF是正方形.
【解析】(1)由已知MN∥BC,CE、CF分别平分∠BCO和∠GCO,可推出∠OEC=∠OCE,∠OFC=∠OCF,所以得EO=CO=FO.(2)菱形的判定问题,若使菱形,则必有四条边相等,对角线互相垂直.(3)由(1)得出的EO=CO=FO,点O运动到AC的中点时,则由EO=CO=FO=AO,所以这时四边形AECF是矩形.(4)由已知和(3)得到的结论,点O运动到AC的中点时,且△ABC满足∠ACB为直角的直角三角形时,则推出四边形AECF是矩形且对角线垂直,所以四边形AECF是正方形.
【考点精析】本题主要考查了菱形的判定方法和矩形的判定方法的相关知识点,需要掌握任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形;有一个角是直角的平行四边形叫做矩形;有三个角是直角的四边形是矩形;两条对角线相等的平行四边形是矩形才能正确解答此题.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:初中数学 来源: 题型:
【题目】初三(1)班12名同学练习定点投篮,每人各投10次,进球数统计如下:
进球数(个) | 1 | 2 | 3 | 4 | 5 | 7 |
人数(人) | 1 | 1 | 4 | 2 | 3 | 1 |
这12名同学进球数的众数是( )
A.3.75
B.3
C.3.5
D.7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一天李小虎同学用“几何画板”画图,他先画了两条平行线AB,CD,然后在平行线间画了一点E,连接BE,DE后(如图①),他用鼠标左键点住点E,拖动后,分别得到如图②,③,④等图形,这时他突然一想,∠B,∠D与∠BED之间的度数有没有某种联系呢?接着小虎同学通过利用“几何画板”的“度量角度”和“计算”功能,找到了这三个角之间的关系.
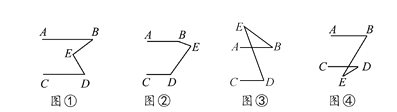
(1)你能探究出图①到图④各图中的∠B,∠D与∠BED之间的关系吗?
(2)请从所得的四个关系中,选一个说明它成立的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】人体中红细胞的直径约为0.0000077m,将数0.0000077用科学记数法表示为( )
A.77×10﹣5
B.0.77×10﹣7
C.7.7×10﹣6
D.7.7×10﹣7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某城市按以下规定收取每月的水费:用水不超过10立方米,按每立方米2.1元收费;如果超过10立方米,超过部分按每立方米3元收费,已知某用户l2月水费平均每立方米2.5元.
按要求回答下列问题:
(l)这个用户12月用水量____10立方米(填“超过”或“不超过”).
(2)在(1)的前提下,求12月这个用户的用水量是多少立方米?
(3)该用户12月份需交水费____元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形纸片ABCD,点E、F分别在边AB、CD上,连接EF,将∠BEF对折点B落在直线EF上的点B′处,得折痕EM;将∠AEF对折,点A落在直线EF上的点A′处,得折痕EN,求∠NEM的度数,并直接写出∠B′ME互余的角.
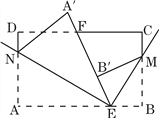
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com