
【题目】在正方形 ABCD 中,M 是 BC 边上一点,且点 M 不与 B、C 重合,点 P 在射线 AM 上,将线段 AP 绕点 A 顺时针旋转 90°得到线段 AQ,连接BP,DQ.
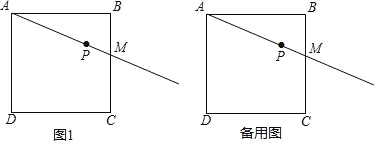
(1)依题意补全图 1;
(2)①连接 DP,若点 P,Q,D 恰好在同一条直线上,求证:DP2+DQ2=2AB2;
②若点 P,Q,C 恰好在同一条直线上,则 BP 与 AB 的数量关系为: .
【答案】(1)详见解析;(2)①详见解析;②BP=AB.
【解析】
(1)根据要求画出图形即可;
(2)①连接BD,如图2,只要证明△ADQ≌△ABP,∠DPB=90°即可解决问题;
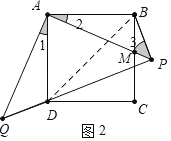
②结论:BP=AB,如图3中,连接AC,延长CD到N,使得DN=CD,连接AN,QN.由△ADQ≌△ABP,△ANQ≌△ACP,推出DQ=PB,∠AQN=∠APC=45°,由∠AQP=45°,推出∠NQC=90°,由CD=DN,可得DQ=CD=DN=AB;
(1)解:补全图形如图 1:
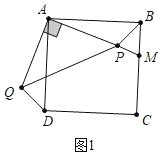
(2)①证明:连接 BD,如图 2,
∵线段 AP 绕点 A 顺时针旋转 90°得到线段 AQ,
∴AQ=AP,∠QAP=90°,
∵四边形 ABCD 是正方形,
∴AD=AB,∠DAB=90°,
∴∠1=∠2.
∴△ADQ≌△ABP,
∴DQ=BP,∠Q=∠3,
∵在 Rt△QAP 中,∠Q+∠QPA=90°,
∴∠BPD=∠3+∠QPA=90°,
∵在 Rt△BPD 中,DP2+BP2=BD2, 又∵DQ=BP,BD2=2AB2,
∴DP2+DQ2=2AB2.
②解:结论:BP=AB.
理由:如图 3 中,连接 AC,延长 CD 到 N,使得 DN=CD,连接 AN,QN.

∵△ADQ≌△ABP,△ANQ≌△ACP,
∴DQ=PB,∠AQN=∠APC=45°,
∵∠AQP=45°,
∴∠NQC=90°,
∵CD=DN,
∴DQ=CD=DN=AB,
∴PB=AB.


科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,BC为⊙O的切线,D为⊙O上的一点,CD=CB,延长CD交BA的延长线于点E.
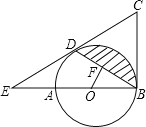
(1)求证:CD为⊙O的切线;
(2)若OF⊥BD于点F,且OF=2,BD=4![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,翻折∠C,使点C落在斜边AB上某一点D处,折痕为EF(点E、F分别在边AC、BC上)

(1)若△CEF与△ABC相似.
①当AC=BC=2时,AD的长为 ;
②当AC=3,BC=4时,AD的长为 ;
(2)当点D是AB的中点时,△CEF与△ABC相似吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:对于抛物线y=ax2+bx+c(a、b、c是常数,a≠0),若b2=ac,则称该抛物线为黄金抛物线.例如:y=x2﹣x+1是黄金抛物线
(1)请再写出一个与上例不同的黄金抛物线的解析式;
(2)将黄金抛物线y=x2﹣x+1沿对称轴向下平移3个单位
①直接写出平移后的新抛物线的解析式;
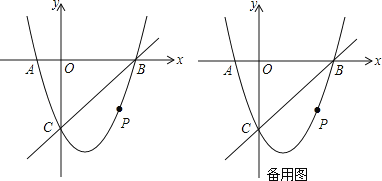
②新抛物线如图所示,与x轴交于A、B(A在B的左侧),与y轴交于C,点P是直线BC下方的抛物线上一动点,连结PO、PC,并把△POC沿CO翻折,得到四边形POP′C,那么是否存在点P,使四边形POP′C为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
③当直线BC下方的抛物线上动点P运动到什么位置时,四边形 OBPC的面积最大并求出此时P点的坐标和四边形OBPC的最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
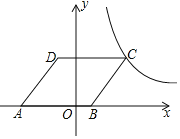
【题目】如图,在平面直角坐标系中,点O为坐标原点,菱形ABCD的顶点B在x轴的正半轴上,点A坐标为(-4,0),点D的坐标为(-1,4),反比例函数![]() 的图象恰好经过点C,则k的值为______.
的图象恰好经过点C,则k的值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中, ![]() ,
,![]() ,
,![]() ,点
,点![]() 是斜边的中点,以点
是斜边的中点,以点![]() 为顶点作
为顶点作![]() ,射线
,射线![]() 、
、![]() 分别交边
分别交边![]() 、
、![]() 于点
于点![]() 、
、![]() .
.
特例
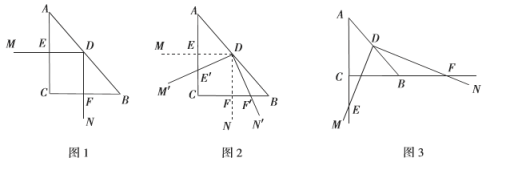
(1)如图1,若![]() ,不添加辅助线,图1中所有与
,不添加辅助线,图1中所有与![]() 相似的三角形为 ,
相似的三角形为 ,![]() ;
;
操作探究:
(2)将(1)中的![]() 从图1的位置开始绕点
从图1的位置开始绕点![]() 按逆时针方向旋转,得到
按逆时针方向旋转,得到![]() ,如图2,当射线
,如图2,当射线![]() ,
,![]() 分别交边
分别交边![]() 、
、![]() 于点
于点![]() 、
、![]() 时,求
时,求![]() 的值;
的值;
拓展延伸:
(3)如图3,![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 是斜边
是斜边![]() 的中点,以点
的中点,以点![]() 为顶点作
为顶点作![]() ,射线
,射线![]() 、
、![]() 分别交边
分别交边![]() 、
、![]() 的延长线于点
的延长线于点![]() 、
、![]() ,则
,则![]() 的值为 .(用含
的值为 .(用含![]() 、
、![]() 的代数式表示,直接回答即可)
的代数式表示,直接回答即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线的对称轴是直线x=1,与x轴有两个交点,与y轴交点的坐标为(0,3),把它向下平移2个单位后,得到新的抛物线的解析式是y=ax2+bx+c,以下四个结论:①b2-4ac<0;②abc<0;③4a+2b+c=1;④a-b+c>0,其中正确的是
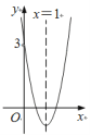
A.①②③B.②③④C.①③④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在菱形ABCD中,∠BAD=α,E为对角线AC上的一点(不与A,C重合)将射线EB绕点E顺时针旋转β角之后,所得射线与直线AD交于F点.试探究线段EB与EF的数量关系.
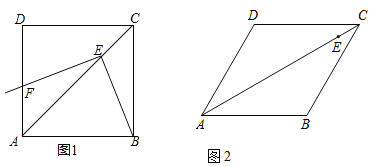
(1)如图1,当α=β=90°时,EB与EF的数量关系为 ;
(2)如图2,当α=60°,β=120°时,
①依题意补全图形;
②探究(1)的结论是否成立,若成立,请给出证明;若不成立,请举出反例证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com