
【题目】定义:对于抛物线y=ax2+bx+c(a、b、c是常数,a≠0),若b2=ac,则称该抛物线为黄金抛物线.例如:y=x2﹣x+1是黄金抛物线
(1)请再写出一个与上例不同的黄金抛物线的解析式;
(2)将黄金抛物线y=x2﹣x+1沿对称轴向下平移3个单位
①直接写出平移后的新抛物线的解析式;
②新抛物线如图所示,与x轴交于A、B(A在B的左侧),与y轴交于C,点P是直线BC下方的抛物线上一动点,连结PO、PC,并把△POC沿CO翻折,得到四边形POP′C,那么是否存在点P,使四边形POP′C为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
③当直线BC下方的抛物线上动点P运动到什么位置时,四边形 OBPC的面积最大并求出此时P点的坐标和四边形OBPC的最大面积.
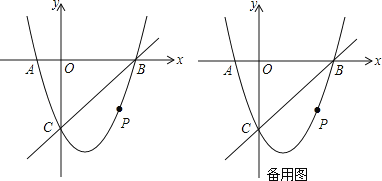
【答案】(1)y=x2+x+1;(2)①:y=x2﹣x﹣2;②存在P点的坐标为(![]() ,﹣1);当x=1时,最大值是3,P(1,﹣2)
,﹣1);当x=1时,最大值是3,P(1,﹣2)
【解析】
(1)直接根据黄金抛物线的定义写一个解析式即可;
(2)①根据平移的知识直接写出新抛物线的解析式;
②设P点坐标为(x,x2﹣x﹣2),PP′交CO于E,若四边形POP′C是菱形,则有PC=PO,连结PP′则PE⊥CO于E,P点的横坐标为﹣1,进而解方程求出x的值;
③过点P作y轴的平行线与BC交于点Q,与OB交于点F,设P(x,x2﹣x﹣2),先求出BC的直线解析式,进而设Q点的坐标为(x,x﹣2),根据S四边形OBPC=S△OBC+S△BPQ+S△CPQ列出x的二次函数解析式,根据二次函数的性质求出满足条件的P点坐标以及面积最大值.
解:(1)不唯一,例如:y=x2+x+1;
(2)①:y=x2﹣x﹣2;
②存在点P,如图1,使四边形POP′C为菱形.
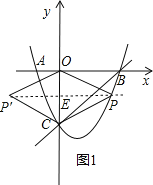
设P点坐标为(x,x2﹣x﹣2),PP′交CO于E
若四边形POP′C是菱形,则有PC=PO.
连结PP′则PE⊥CO于E,
∴OE=EC=1,
∴y=﹣1,
∴x2﹣x﹣2=﹣1
解得x1=![]() ,x2=
,x2=![]() (不合题意,舍去)
(不合题意,舍去)
∴P点的坐标为(![]() ,﹣1);
,﹣1);
③过点P作y轴的平行线与BC交于点Q,与OB交于点F,如图2
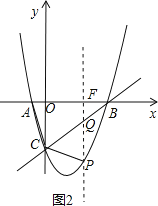
设P(x,x2﹣x﹣2),
易得,直线BC的解析式:y=x﹣2
则Q点的坐标为(x,x﹣2).
S四边形OBPC=S△OBC+S△BPQ+S△CPQ
=![]() OBOC+
OBOC+![]() QPOF+
QPOF+![]() QPFB=
QPFB=![]()
=﹣(x﹣1)2+3,
当x=1时,四边形OBPC的面积最大
此时P点的坐标为(1,﹣2),
四边形OBPC的面积最大值是3.


科目:初中数学 来源: 题型:
【题目】有三张正面分别标有数字:-1,1,2的卡片,它们除数字不同外其余全部相同,现将它们背面朝上,洗匀后从中随机抽出一张记下数字,放回洗匀后再从中随机抽出一张记下数字.
(1)请用列表或画树形图的方法(只选其中一种),表示两次抽出卡片上的数字的所有结果;
(2)将第一次抽出的数字作为点的横坐标x,第二次抽出的数字作为点的纵坐标y,求点(x,y)落在双曲线![]() 上的概率.
上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=x2的图象如图,点A0位于坐标原点,点A1,A2,A3…An在y轴的正半轴上,点B1,B2,B3…Bn在二次函数位于第一象限的图象上,点C1,C2,C3…n在二次函数位于第二象限的图象上,四边形A0B1A1C1,四边形A1B2A2C2,四边形A2B3A3C3…四边形An﹣1BnAnn都是正方形,则正方形An﹣1BnAnn的周长为_____.
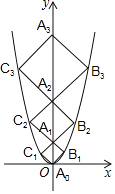
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】Rt△ABC中,∠ABC=90°,AB=3,BC=4,过点B的直线把△ABC分割成两个三角形,使其中只有一个是等腰三角形,则这个等腰三角形的面积是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,将矩形ABCD折叠,使BC落在对角线BD上,折痕为BE,点C落在点C′处,若∠ADB=46°,则∠DBE的度数为 °.
(2)小明手中有一张矩形纸片ABCD,AB=4,AD=9.
(画一画)
如图2,点E在这张矩形纸片的边AD上,将纸片折叠,使AB落在CE所在直线上,折痕设为MN(点M,N分别在边AD,BC上),利用直尺和圆规画出折痕MN(不写作法,保留作图痕迹,并用黑色水笔把线段描清楚);
(算一算)
如图3,点F在这张矩形纸片的边BC上,将纸片折叠,使FB落在射线FD上,折痕为GF,点A,B分别落在点A′,B′处,若AG=![]() ,求B′D的长;
,求B′D的长;
(验一验)
如图4,点K在这张矩形纸片的边AD上,DK=3,将纸片折叠,使AB落在CK所在直线上,折痕为HI,点A,B分别落在点A′,B′处,小明认为B′I所在直线恰好经过点D,他的判断是否正确,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形 ABCD 中,M 是 BC 边上一点,且点 M 不与 B、C 重合,点 P 在射线 AM 上,将线段 AP 绕点 A 顺时针旋转 90°得到线段 AQ,连接BP,DQ.
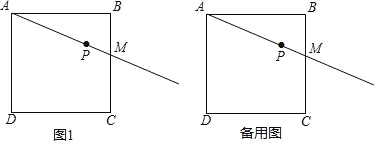
(1)依题意补全图 1;
(2)①连接 DP,若点 P,Q,D 恰好在同一条直线上,求证:DP2+DQ2=2AB2;
②若点 P,Q,C 恰好在同一条直线上,则 BP 与 AB 的数量关系为: .
查看答案和解析>>
科目:初中数学 来源: 题型:
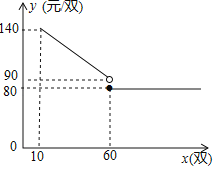
【题目】立定跳远是嘉兴市体育中考的抽考项目之一,某校九年级(1),(2)班准备集体购买某品牌的立定跳远训练鞋.现了解到某网店正好有这种品牌训练鞋的促销活动,其购买的单价y(元/双)与一次性购买的数量x(双)之间满足的函数关系如图所示.
(1)当10≤x<60时,求y关于x的函数表达式;
(2)九(1),(2)班共购买此品牌鞋子100双,由于某种原因需分两次购买,且一次购买数量多于25双且少于60双;
①若两次购买鞋子共花费9200元,求第一次的购买数量;
②如何规划两次购买的方案,使所花费用最少,最少多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
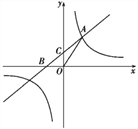
【题目】如图15,直线y=x+b与双曲线y=![]() 都经过点A(2,3),直线y=x+b与x轴、y轴分别交于B、C两点.
都经过点A(2,3),直线y=x+b与x轴、y轴分别交于B、C两点.
(1)求直线和双曲线的函数关系式;
(2)求△AOB的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com