
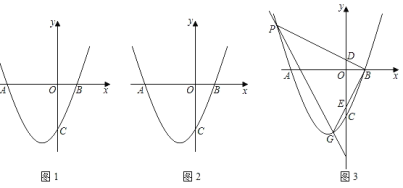
����Ŀ����ͼ1��������������y��x2ƽ�ƺ�õ������Ķ�������Ϊ����![]() ����
����![]() ��������������ֱ���A��B��C���㣮
��������������ֱ���A��B��C���㣮
��1����A��B�����꣮
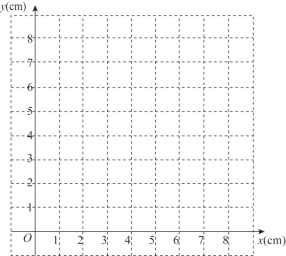
��2����ͼ2������BC��AC���ڵ�����������������һ��P��ʹ��PCA����BCO�����P�����꣮
��3����ͼ3��ֱ��y��ax+b��b��0����������߷ֱ���P��G���㣬����BP��BG�ֱ�y���ڵ�D��E����ODOE��3����̽��a��b��������ϵ����˵�����ɣ�
���𰸡���1��![]() ����2��
����2��![]() ����3��b��4a+3�����ɼ�������
����3��b��4a+3�����ɼ�������
��������
��1�����ݶ�������д������ʽ��������ʽΪһ��ʽ���ֱ���x=0��y=0�������A��B�����ꣻ
��2��ֱ��CP��x���ڵ�H���ʵ�H��HG��AC��AC���ӳ����ڵ�G������tan��BCO��tan��PCA��ֱ�������μ������H�����꣬�ɴ˿����ֱ��CH�ı���ʽ���������κ�������ʽ������õ�P���ꣻ
��3��ֱ��BP�ı���ʽΪ��y=��m+4��x-��m+4����ֱ��BG�ı���ʽΪ��y=��n+4��x-��n+4������OD=-��m+4����OE=��n+4����ODOE=-��m+4����n+4��=3����-[mn+4��m+n��+16]=3����m+n=a-3��mn=-b-4��������⣮
�⣺��1�������ߵı���ʽΪ��y����x+![]() ��2��
��2��![]() ��x2+3x��4���٣�
��x2+3x��4���٣�
��x��0����y����4���ʵ�C��0����4����
��y��0����x��-4��1��
�ʵ�A��B������ֱ�Ϊ������4��0������1��0����
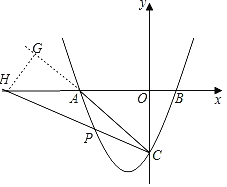
��2����ͼ����ֱ��CP��x���ڵ�H���ʵ�H��HG��AC��AC���ӳ����ڵ�G��
tan��BCO��![]() ��
��![]() ��tan��PCA��
��tan��PCA��
��OA��OC��4���ʡ�BAC��45������GAH��
��GH��GA��x����GC��4x����AC��GC��GA��3x��4![]() ��
��
��ã�x��![]() ��
��
��AH��![]() x��
x��![]() ���ʵ�H����
���ʵ�H����![]() ��0����
��0����
��CH�ı���ʽΪ��y��kx+b��
��C��H����������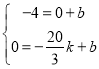 �����
�����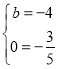 ��
��
��CH�ı���ʽΪ��y����![]() x��4���ڣ�
x��4���ڣ�
�����٢ڲ���ã�x��0����ȥ����![]() ��
��
�ʵ�P����![]() ����
����![]() ����
����
��3�����P��G������ֱ�Ϊ����m��m2+3m��4������n��n2+3n��4����
�ɵ�P��B������ã�ֱ��PB�ı���ʽΪ��y����m+4��x����m+4����
ͬ��ֱ��BG�ı���ʽΪ��y����n+4��x����n+4����
��OD������m+4����OE����n+4����
ֱ��y��ax+b��b��0�����ۣ�
�����٢۲������ã�x2+��3��a��x��b��4��0��
��m+n��a��3��mn����b��4��
ODOE������m+4����n+4����3��
����[mn+4��m+n��+16]��3����m+n��a��3��mn����b��4��
�����ã�b��4a+3��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
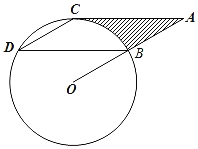
����Ŀ����ͼ����B��C��D������O�ϣ�����C��AC��BD��OB���ӳ����ڵ�A������CD���ҡ�CDB����OBD��30�㣬BD��6![]() cm��
cm��
��1����֤��AC����O�����ߣ�
��2������O�İ뾶����
��3����ͼ����Ӱ���ֵ�������������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
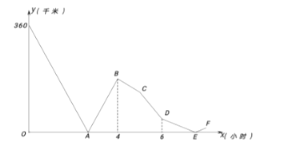
����Ŀ�����������ֱ�����![]() ǧ�ļס�������ͬʱ������������ʻ��;�����������ͣ��
ǧ�ļס�������ͬʱ������������ʻ��;�����������ͣ��![]() Сʱ��Ȼ�� ��ԭ�ٶȵ�
Сʱ��Ȼ�� ��ԭ�ٶȵ�![]() �����������ʻ������غ�ֹͣ��ʻ���쳵���ٵ����ҵغ�������ԭ·ԭ�ٷ��ؼ� �أ��쳵��ͷʱ����Բ��ƣ������ұ�������ǰ
�����������ʻ������غ�ֹͣ��ʻ���쳵���ٵ����ҵغ�������ԭ·ԭ�ٷ��ؼ� �أ��쳵��ͷʱ����Բ��ƣ������ұ�������ǰ![]() ���ӵ���أ���������֮��ľ���
���ӵ���أ���������֮��ľ���![]() ��ǧ�ף���� ����ʻʱ��
��ǧ�ף���� ����ʻʱ��![]() ��Сʱ��֮��ĺ���ͼ����ͼ��ʾ���������ڶ�������ʱ��������ػ���________ǧ�ף�
��Сʱ��֮��ĺ���ͼ����ͼ��ʾ���������ڶ�������ʱ��������ػ���________ǧ�ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��P���߶�AB�ϵ�һ�㣬AB=6cm��O��AB��һ���㣮����OP����OP�Ƶ�O˳ʱ����ת120����OQ������PQ��AQ��
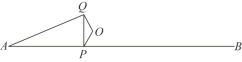
С������ѧϰ�����ľ��飬���߶�AP��PQ��AQ�ij���֮��Ĺ�ϵ������̽����
������С����̽�����̣��벹��������
��1�����ڵ�P��AB�ϵIJ�ͬλ�ã���ͼ���������õ����߶�AP��PQ��AQ�ij��ȣ���λ��cm���ļ���ֵ�����±���
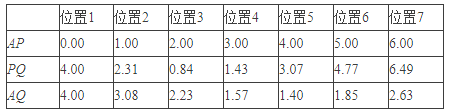
��AP��PQ��AQ�ij������������У�ȷ��________�ij������Ա�����________�ij��Ⱥ�________�ij��ȶ�������Ա����ĺ�����
��2����ͬһƽ��ֱ������ϵxOy�У�������1������ȷ���ĺ�����ͼ��
��3����Ϻ���ͼ������⣺��AQ=PQʱ���߶�AP�ij���ԼΪ________cm��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y��kx+b��k��0����ͼ���뷴��������y��![]() ��m��0��x��0����ͼ���ڵ�һ�����ڽ��ڵ�A��B���Ҹ�һ�κ�����ͼ����y�������ύ�ڵ�C����A��B�ֱ���y��Ĵ��ߣ�����ֱ�ΪD��E����֪A��1��4����
��m��0��x��0����ͼ���ڵ�һ�����ڽ��ڵ�A��B���Ҹ�һ�κ�����ͼ����y�������ύ�ڵ�C����A��B�ֱ���y��Ĵ��ߣ�����ֱ�ΪD��E����֪A��1��4����![]() ��
��![]() ��
��
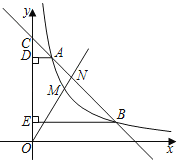
��1����m��ֵ��һ�κ����Ľ���ʽ��
��2������MΪ����������ͼ����A��B֮��Ķ��㣬������OM��ֱ��AB�ڵ�N����MN�������ʱ��ֱ��д����M�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ��չ�ˡ�������ƽ�ȡ��ж�����г����ȡ������������ͻ��
5����������˳������飨ÿλͬѧֻѡȡ���ע��һ���������ݵ�������������������
����ͳ��ͼ������ͼ���ṩ����Ϣ������������⣺
��1����ε����ѧ�����ж�������
��2���뽫����ͳ��ͼ����������
��3��������ͳ��ͼ�С���ȡ���������ε�Բ�Ľ����� ���ȣ�
��4������Уѧ������Ϊ800�ˣ���������������������Ƹ�Уѧ���С��ж�����������
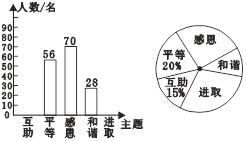
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
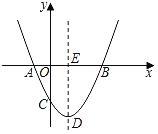
����Ŀ����ͼ��������y��ax2+bx+c�Ķ���ΪD����x�ύ��A��B�ĺ�����ֱ�Ϊ��1��3����y�Ḻ���ύ�ڵ�C������������ۣ�
��2a+b��0��
��4a+2b+c��0��
��������ʵ��x��ax2+bx��a+b��
��ֻ�е�a��![]() ʱ����ABD�ǵ���ֱ�������Σ�
ʱ����ABD�ǵ���ֱ�������Σ�
��ʹ��ABCΪ���������ε�aֵ������3����
������ȷ�Ľ�����_____��������ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ABC����ACB��90�㣬BC��3��AC��4��С�찴���²�����ͼ��
���ֱ���A��CΪԲ�ģ��Դ���![]() AC�ij�Ϊ�뾶��AC������������������M��N��
AC�ij�Ϊ�뾶��AC������������������M��N��
������MN���ֱ�AB��AC�ڵ�D��O��
����C��CE��AB��MN�ڵ�E������AE��CD��
���ı���ADCE���ܳ�Ϊ��������

A. 10 B. 20 C. 12 D. 24
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��10��10�������У�A��B��C���ڸ���ϣ�ڽ���̶ȵ�ֱ����ֱ��MN��ʹ��ֱ��MNƽ����ABC���ܳ�������ͼ�ۼ�����д������
��1������ͼ1����������Ҫ���һ��ֱ��MN��
��2����ͼ2����MΪBC��һ�㣬BM��5������AB��������N��λ�ã�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com