
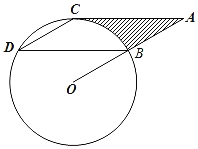
【题目】如图,点B、C、D都在⊙O上,过点C作AC∥BD交OB的延长线于点A,连接CD,且∠CDB=∠OBD=30°,BD=6![]() cm.
cm.
(1)求证:AC是⊙O的切线.
(2)求⊙O的半径长.
(3)求图中阴影部分的面积(结果保留π).
【答案】(1)详见解析;(2)6;(3)(![]() )cm2.
)cm2.
【解析】
(1)连接OC,根据圆周角定理得到∠BOC=60°,根据平行线的性质得到∠A=∠OBD=30°,于是求得∠ACO=90°,根据切线的判定定理即可得到结论;
(2)设OC交BD于E,由(1)得,OC⊥AC,根据平行线的性质得到OC⊥BD,求得BD=6![]() ,解直角三角形即可得到结论;
,解直角三角形即可得到结论;
(3)根据平行线的判定定理得到OA∥CD,推出四边形ABDC是平行四边形,求得AC=BD=6![]() ,根据三角形和扇形的面积公式即可得到结论.
,根据三角形和扇形的面积公式即可得到结论.
(1)证明:如图,连接OC,
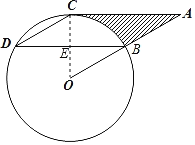
∵∠CDB=∠OBD=30°,
∴∠BOC=60°.
∵AC∥BD,
∴∠A=∠OBD=30°,
∴∠BOC+∠A=90°.
∴∠ACO=90°.
又∵点C在⊙O上,
∴AC为⊙O切线;
(2)解:设OC交BD于E,
由(1)得,OC⊥AC,
∵AC∥BD,
∴OC⊥BD,
∴E为BD的中点,
∵BD=![]() ,
,
∴BE=![]() ,
,
在Rt△OBE中,![]() ,
,
即![]() ,
,
∴![]() ,
,
解得OB=6,
即⊙O的半径长为6cm;
(3)∵∠CDB=∠OBD,
∴OA∥CD,
∵AC∥BD,
∴四边形ABDC是平行四边形,
∴AC=BD=6![]() ,
,
∴![]()
=![]() .
.
答:阴影部分的面积为(![]() )cm2.
)cm2.


 优等生题库系列答案
优等生题库系列答案科目:初中数学 来源: 题型:
【题目】定义一种对正整数n的“F”运算:①当n为奇数时,F(n)=3n+1;②当n为偶数时,F(n)=![]() (其中k是使F(n)为奇数的正整数)…,两种运算交替重复进行,例如,取n=24,则:若n=14,则第2019次“F”运算的结果是( )
(其中k是使F(n)为奇数的正整数)…,两种运算交替重复进行,例如,取n=24,则:若n=14,则第2019次“F”运算的结果是( )
![]()
A.4B.1C.2018D.42018
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下说法正确的是( )
A.小明做了![]() 次掷图钉的实验,发现
次掷图钉的实验,发现![]() 次钉尖朝上,由此他说钉尖朝上的概率是
次钉尖朝上,由此他说钉尖朝上的概率是![]()
B.一组对边平行,另一组对边相等的四边形是平行四边形
C.点![]() 都在反比例函数
都在反比例函数![]() 图象上,且
图象上,且![]() 则
则![]() ;
;
D.对于一元二元方程![]() ,若
,若![]() 则方程的两个根互为相反数
则方程的两个根互为相反数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】揭西县围绕“推进‘六稳’,拉动消费”为主题,举办“揭西人游揭西”活动,从4月份到6月份,分批次免费游览县内相关旅游景区景点.某班级全班同学分别从A、B、C、D、E五个景区中选出自己最喜欢的一个,绘制出如下的统计图①和图②,请根据相关信息,解答下列问题:
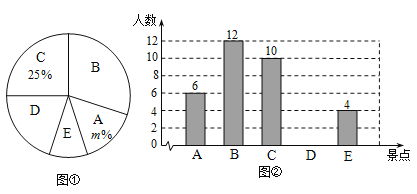
(1)图①中m的值为.扇形统计图中,B景区所对的圆心角的大小是;
(2)补全条形统计图;
(3)甲乙两个同学分别从A、B、C、D四个景区中随机挑出一个景区各自游玩,请用树状图或列表的方法求出他们刚好选到同一个景区的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在完善基础设施、改善市容市貌、提升城市品质过程中,2019年我市开展人行道改造工程,需要花岗岩地板砖铺设人行道.现租用甲、乙两种货车运载地板砖,已知一辆甲车每次运载的重量比一辆乙车多2吨,且甲车运载16吨地板砖和乙车运载12吨地板砖所用的车辆数相同.
(1)甲、乙两种货车每次运载地板砖各多少吨?
(2)现租用甲车a辆、乙车b辆,刚好运载地板砖100吨,且a≤3b,共有多少种租车方案?
(3)在(2)中已知一辆甲车每次的运费是380元,一辆乙车每次的运费是300元,如何租用甲、乙两种车可使得总运费最低?求出最低总运费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD,两条对角线相交于O点,过点O作AC的垂线EF,分别交AD、BC于E、F点,连结CE,若OC![]() cm,CD=4cm,则DE的长为( )
cm,CD=4cm,则DE的长为( )
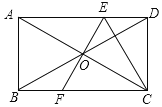
A.![]() cmB.5cmC.3cmD.2cm
cmB.5cmC.3cmD.2cm
查看答案和解析>>
科目:初中数学 来源: 题型:
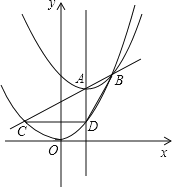
【题目】A是直线x=1上一个动点,以A为顶点的抛物线y1=a(x﹣1)2+t和抛物线y2=ax2交于点B(A,B不重合,a是常数),直线AB和抛物线y2=ax2交于点B,C,直线x=1和抛物线y2=ax2交于点D.(如图仅供参考)
(1)求点B的坐标(用含有a,t的式子表示);
(2)若a<0,且点A向上移动时,点B也向上移动,求![]() 的范围;
的范围;
(3)当B,C重合时,求![]() 的值;
的值;
(4)当a>0,且△BCD的面积恰好为3a时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
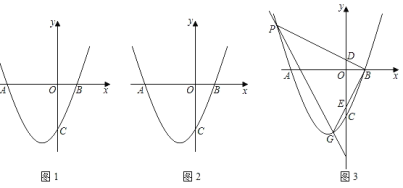
【题目】如图1,该抛物线是由y=x2平移后得到,它的顶点坐标为(﹣![]() ,﹣
,﹣![]() ),并与坐标轴分别交于A,B,C三点.
),并与坐标轴分别交于A,B,C三点.
(1)求A,B的坐标.
(2)如图2,连接BC,AC,在第三象限的抛物线上有一点P,使∠PCA=∠BCO,求点P的坐标.
(3)如图3,直线y=ax+b(b<0)与该抛物线分别交于P,G两点,连接BP,BG分别交y轴于点D,E.若ODOE=3,请探索a与b的数量关系.并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com