
����Ŀ��������Χ�ơ��ƽ������ȡ����������ѡ�Ϊ���⣬�ٰ조�������ν����������4�·ݵ�6�·ݣ������������������������ξ������㣮ij�༶ȫ��ͬѧ�ֱ��A��B��C��D��E���������ѡ���Լ���ϲ����һ�������Ƴ����µ�ͳ��ͼ�ٺ�ͼ�ڣ�����������Ϣ������������⣺
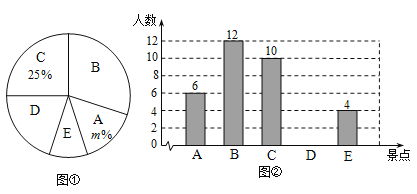
��1��ͼ����m��ֵΪ������ͳ��ͼ�У�B�������Ե�Բ�ĽǵĴ�С�ǣ�
��2����ȫ����ͳ��ͼ��
��3����������ͬѧ�ֱ��A��B��C��D�ĸ��������������һ�������������棬������״ͼ���б��ķ���������Ǹպ�ѡ��ͬһ�������ĸ��ʣ�
���𰸡���1��15��108�㣻��2������������3��![]()
��������
(1)�ȸ���C��ռ�İٷֱ��Լ�C������������ܵ����������ټ���m��ֵ�Լ�B�������Ե�Բ�ĽǴ�С���ɵõ��𰸣�
(2)�ȸ����ܵ����������D�������������ٲ�ȫͼ�μ��ɣ�
(3)�ñ������������оٳ������ٸ��ݸ��ʹ�ʽ��⼴�ɵõ��𰸣�
��1���ܵ�������Ϊ��10��25��=40�ˣ�
��A��ռ�İٷֱ�Ϊ��![]() ��
��
B�������Ե�Բ�ĽǵĴ�С�ǣ�![]() ��
��
�ʴ�Ϊ��15��108�㣻
��2��D����������Ϊ��40-6-12-10-4=8�ˣ�
��ȫ����ͳ��ͼ����ͼ

��3�����Կ��ܳ����ڽ�����±�
���� | A | B | C | D |
A | ��A��A�� | ��A��B�� | ��A��C�� | ��A��D�� |
B | ��B��A�� | ��B��B�� | ��B��C�� | ��B��D�� |
C | ��C��A�� | ��C��B�� | ��C��C�� | ��C��D�� |
D | ��D��A�� | ��D��B�� | ��D��C�� | ��D��D�� |
���������ɵ��ܹ���16�ֿ��ܣ����м��Ҹպ�ѡ��ͬһ�������������֣�
��A��A����B��B����C��C����D��D�����ʸ���Ϊ![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ѧϰ��Բ����һ��Ԫʱ������ѧϰ��Բ�ܽǶ��������ۣ�Բ�ڽ��ı��εĶԽǻ�������ʵ�ϣ����������⣺�Խǻ������ı��ε��ĸ����㹲Բ��Ҳ��һ�������⣮��ͼ����ת���ۺ����о�������ֶԽǻ������ı��Σ���ô�����ǾͿ��Խ������Խǻ������ı��ε��ĸ����㹲Բ����Ȼ�����Բ�����֪ʶ��������⣬���磺
��֪��![]() �ǵȱ������Σ���
�ǵȱ������Σ���![]() ��
��![]() ��һ�㣬����
��һ�㣬����![]() �����߶�
�����߶�![]() ��
��![]() ��ʱ����ת
��ʱ����ת![]() �õ��߶�
�õ��߶�![]() ������
������![]() ��
��![]() ��
��![]() �����ӳ�
�����ӳ�![]() ��
��![]() �ڵ�
�ڵ�![]() ������
������![]() ����ͼ��ʾ��λ��ʱ��
����ͼ��ʾ��λ��ʱ��
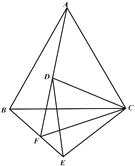
��1���۲���գ�
����![]() ȫ�ȵ���������________��
ȫ�ȵ���������________��
��![]() �Ķ���Ϊ��������������
�Ķ���Ϊ��������������
��2����������еĽ��ۣ�֤����![]() ��
��![]() ��
��![]() ��
��![]() �ĵ㹲Բ��
�ĵ㹲Բ��
��3��ֱ��д���߶�![]() ��
��![]() ��
��![]() ֮���������ϵ��____________________��
֮���������ϵ��____________________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
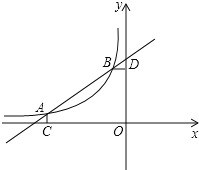
����Ŀ����ͼ����֪A(��3��![]() )��B(��1��m)��һ�κ���y��kx+b�뷴��������y��
)��B(��1��m)��һ�κ���y��kx+b�뷴��������y��![]() ͼ����������㣬AC��x���ڵ�C��BD��y���ڵ�D��
ͼ����������㣬AC��x���ڵ�C��BD��y���ڵ�D��
��1����m��ֵ��һ�κ�������ʽ��
��2��P���߶�AB�ϵ�һ�㣬����PC��PD������PCA����PDB�����ȣ����P���꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
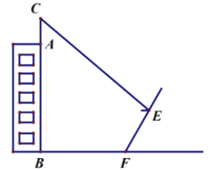
����Ŀ����ͼ��ijУ��һ��ѧ¥![]() ��������һ������
��������һ������![]() Ϊ
Ϊ![]() �ף���ѧ¥������һСɽ�����¶�Ϊ
�ף���ѧ¥������һСɽ�����¶�Ϊ![]() ɽ������һ��Ϣͤ
ɽ������һ��Ϣͤ![]() ����ɽ��Ա��Ϣ�����ɽ�½�
����ɽ��Ա��Ϣ�����ɽ�½�![]() ���ѧ§��ˮƽ����
���ѧ§��ˮƽ����![]() Ϊ
Ϊ![]() �ף�����Ϣͤ�ľ���
�ף�����Ϣͤ�ľ���![]() Ϊ
Ϊ![]() �ף�����Ϣͤ
�ף�����Ϣͤ![]() ��ý�ѧ¥�ϱ����붥��
��ý�ѧ¥�ϱ����붥��![]() ������Ϊ
������Ϊ![]() �����ѧ§
�����ѧ§![]() �ĸ߶ȣ��������������)(ע���¶�
�ĸ߶ȣ��������������)(ע���¶�![]() ��ָ�����Ǧֱ�߶���ˮƽ���ȵıȣ�
��ָ�����Ǧֱ�߶���ˮƽ���ȵıȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y=kx+3��ͼ���뷴��������![]() ��ͼ����P��Q���㣬PA��x���ڵ�A��һ�κ�����ͼ��ֱ�x�ᡢy���ڵ�C����B������OA=6����
��ͼ����P��Q���㣬PA��x���ڵ�A��һ�κ�����ͼ��ֱ�x�ᡢy���ڵ�C����B������OA=6����![]() .
.
(1)��һ�κ����ͷ����������ı���ʽ��
(2)����APQ�������
(3)����ͼ��д����xȡ��ֵʱ��һ�κ�����ֵС�ڷ�����������ֵ.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����У���ṩѧ������������������棬��У�ڶ�ȫУѧ�������˳������飬ÿλѧ��ֻѡ��һ���Լ���ϲ���������˶������У�![]() ������ϲ���μӱ�ƹ���˶���
������ϲ���μӱ�ƹ���˶���![]() ������ϲ���μ���ë���˶���
������ϲ���μ���ë���˶���![]() ������ϲ���������˶���
������ϲ���������˶���![]() ������ϲ�������˶�����ͼ������δ��ɵ�����ͳ��ͼ������ͳ��ͼ������ͳ��ͼ����������Ϣ�������������ϲ�������˶�(��
������ϲ�������˶�����ͼ������δ��ɵ�����ͳ��ͼ������ͳ��ͼ������ͳ��ͼ����������Ϣ�������������ϲ�������˶�(��![]() )�İٷ�����������(����)
)�İٷ�����������(����)

A.24��26%B.33��26.4%C.28��22.4%D.25��23.6%
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
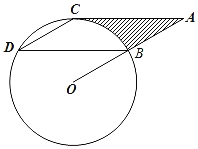
����Ŀ����ͼ����B��C��D������O�ϣ�����C��AC��BD��OB���ӳ����ڵ�A������CD���ҡ�CDB����OBD��30�㣬BD��6![]() cm��
cm��
��1����֤��AC����O�����ߣ�
��2������O�İ뾶����
��3����ͼ����Ӱ���ֵ�������������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�٣�ABΪ��Բ��ֱ����OΪԲ�ģ�CΪԲ����һ�㣬AD��ֱ�ڹ�C������ߣ�����ΪD��AB���ӳ��߽�ֱ��CD�ڵ�E��
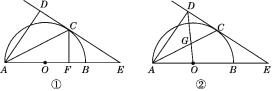
��1����֤��ACƽ�֡�DAB��
��2����AB��6��BΪOE���е㣬CF��AB������Ϊ��F����CF�ij���
��3����ͼ�ڣ�����OD��AC�ڵ�G����![]() ��
��![]() ����cosE��ֵ��
����cosE��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��P���߶�AB�ϵ�һ�㣬AB=6cm��O��AB��һ���㣮����OP����OP�Ƶ�O˳ʱ����ת120����OQ������PQ��AQ��
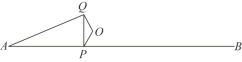
С������ѧϰ�����ľ��飬���߶�AP��PQ��AQ�ij���֮��Ĺ�ϵ������̽����
������С����̽�����̣��벹��������
��1�����ڵ�P��AB�ϵIJ�ͬλ�ã���ͼ���������õ����߶�AP��PQ��AQ�ij��ȣ���λ��cm���ļ���ֵ�����±���
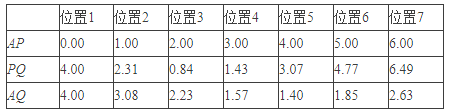
��AP��PQ��AQ�ij������������У�ȷ��________�ij������Ա�����________�ij��Ⱥ�________�ij��ȶ�������Ա����ĺ�����
��2����ͬһƽ��ֱ������ϵxOy�У�������1������ȷ���ĺ�����ͼ��
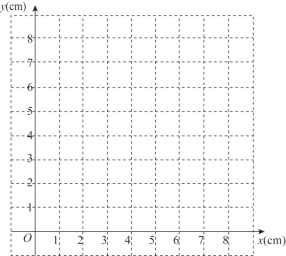
��3����Ϻ���ͼ������⣺��AQ=PQʱ���߶�AP�ij���ԼΪ________cm��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com