
【题目】如图①,AB为半圆的直径,O为圆心,C为圆弧上一点,AD垂直于过C点的切线,垂足为D,AB的延长线交直线CD于点E.
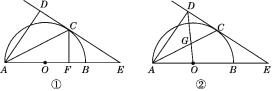
(1)求证:AC平分∠DAB;
(2)若AB=6,B为OE的中点,CF⊥AB,垂足为点F,求CF的长;
(3)如图②,连接OD交AC于点G,若![]() =
=![]() ,求cosE的值.
,求cosE的值.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)连结OC,如图1,根据切线的性质得OC⊥DE,而AD⊥DE,根据平行线的性质得OC∥AD,所以∠2=∠3,加上∠1=∠3,则∠1=∠2,所以AC平分∠DAB;
(2)如图1,由B为OE的中点,AB为直径得到OB=BE=3,OC=3,在Rt△OCE中,由于OE=2OC,根据含30度的直角三角形三边的关系得∠OEC=30°,则∠COE=60°,由CF⊥AB得∠OFC=90°,所以∠OCF=30°,再根据含30度的直角三角形三边的关系得OF=![]() OC=
OC=![]() ,再由勾股定理即可求出CF的长度;
,再由勾股定理即可求出CF的长度;
(3)连结OC,如图2,先证明△OCG∽△DAG,利用相似的性质得![]() =
=![]() =
=![]() ,再证明△ECO∽△EDA,利用相似比得到
,再证明△ECO∽△EDA,利用相似比得到![]() =
=![]() =
=![]() ,设⊙O的半径为R,OE=x,代入求得OE=3R,最后在Rt△OCE中,根据余弦的定义求解.
,设⊙O的半径为R,OE=x,代入求得OE=3R,最后在Rt△OCE中,根据余弦的定义求解.
(1)证明:连结OC,如图1,

∵DE与⊙O切于点C,
∴OC⊥DE,
∵AD⊥DE,
∴OC∥AD,
∴∠2=∠3,
∵OA=OC,
∴∠1=∠3,
∴∠1=∠2,
即AC平分∠DAB;
(2)∵直径AB=6,B为OE的中点,
∴OB=BE=4,OC=3,
在Rt△OCE中,OE=2OC,
∴∠OEC=30°,
∴∠COE=60°,
∵CF⊥AB,
∴∠OFC=90°,
∴∠OCF=30°,
∴OF==![]() OC=
OC=![]() ,
,
∴由勾股定理可知:CF=![]()
(3)连结OC,如图2,
∵OC∥AD,
∴△OCG∽△DAG,
∴![]() =
=![]() =
=![]() ,
,
∵OC∥AD,
∴△ECO∽△EDA,
∴![]() =
=![]() =
=![]() ,
,
设⊙O的半径为R,OE=x,
∴![]() =
=![]() ,解得OE=x=3R,
,解得OE=x=3R,
在Rt△OCE中,
由勾股定理可知:CE=2√2R,
cos∠E=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】数学活动课上,小明同学根据学习函数的经验,对函数的图像、性质进行了探究,下面是小明同学探究过程,请补充完整:
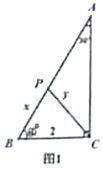
如图1,已知在![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 为
为![]() 边上的一个动点,连接
边上的一个动点,连接![]() .设
.设![]() ,
,![]() .
.
(初步感知)
(1)当![]() 时,则①
时,则①![]() ________,②
________,②![]() ________;
________;
(深入思考)
(2)试求![]() 与
与![]() 之间的函数关系式并写出自变量
之间的函数关系式并写出自变量![]() 的取值范围;
的取值范围;
(3)通过取点测量,得到了![]() 与
与![]() 的几组值,如下表:
的几组值,如下表:
| 0 | 0.5 | 1 | 1.5 | 2. | 2.5 | 3 | 3.5 | 4 |
| 2 | 1.8 | 1.7 | _____ | 2 | 2.3 | 2.6 | 3.0 | _____ |
(说明:补全表格时相关数值保留一位小数)
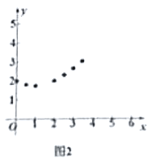
1)建立平面直角坐标系,如图2,描出已补全后的表中各对应值为坐标的点,画出该函数的图象;
2)结合画出的函数图象,写出该函数的两条性质:
①________________________________;②________________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】揭西县围绕“推进‘六稳’,拉动消费”为主题,举办“揭西人游揭西”活动,从4月份到6月份,分批次免费游览县内相关旅游景区景点.某班级全班同学分别从A、B、C、D、E五个景区中选出自己最喜欢的一个,绘制出如下的统计图①和图②,请根据相关信息,解答下列问题:
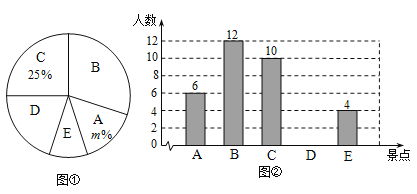
(1)图①中m的值为.扇形统计图中,B景区所对的圆心角的大小是;
(2)补全条形统计图;
(3)甲乙两个同学分别从A、B、C、D四个景区中随机挑出一个景区各自游玩,请用树状图或列表的方法求出他们刚好选到同一个景区的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD,两条对角线相交于O点,过点O作AC的垂线EF,分别交AD、BC于E、F点,连结CE,若OC![]() cm,CD=4cm,则DE的长为( )
cm,CD=4cm,则DE的长为( )
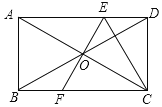
A.![]() cmB.5cmC.3cmD.2cm
cmB.5cmC.3cmD.2cm
查看答案和解析>>
科目:初中数学 来源: 题型:
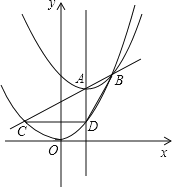
【题目】A是直线x=1上一个动点,以A为顶点的抛物线y1=a(x﹣1)2+t和抛物线y2=ax2交于点B(A,B不重合,a是常数),直线AB和抛物线y2=ax2交于点B,C,直线x=1和抛物线y2=ax2交于点D.(如图仅供参考)
(1)求点B的坐标(用含有a,t的式子表示);
(2)若a<0,且点A向上移动时,点B也向上移动,求![]() 的范围;
的范围;
(3)当B,C重合时,求![]() 的值;
的值;
(4)当a>0,且△BCD的面积恰好为3a时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y![]() x+b的图象与x轴,y轴分别交于A,B两点,与反比例函数y
x+b的图象与x轴,y轴分别交于A,B两点,与反比例函数y![]() (x<0)的图象交于点C(﹣2,2).
(x<0)的图象交于点C(﹣2,2).
(1)求一次函数与反比例函数的表达式;
(2)过点B作x轴的平行线交反比例函数的图象于点D,连接CD.求△BCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
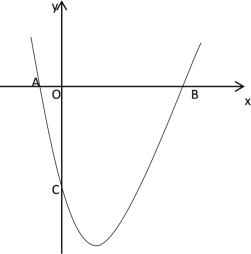
【题目】如图:已知抛物线![]() 与
与![]() 轴,
轴,![]() 轴分别交于点
轴分别交于点![]() ,此抛物线的对称轴为直线
,此抛物线的对称轴为直线![]() .
.
![]() 求出此抛物线的解析式;
求出此抛物线的解析式;
![]() 如图 1,抛物线的顶点为点
如图 1,抛物线的顶点为点![]() ,点
,点![]() 是直线
是直线![]() 下方抛物线上的一点(异于点
下方抛物线上的一点(异于点![]() ),当
),当![]() 时,求出点
时,求出点![]() 的坐标;
的坐标;
![]() 在
在![]() 的条件下,将抛物线沿射线
的条件下,将抛物线沿射线![]() 方向平移,点
方向平移,点![]() 的对应点为
的对应点为![]() ,在抛物线平移的过程中,若
,在抛物线平移的过程中,若![]() ,请直接写出此时平移后的抛物线解析式
,请直接写出此时平移后的抛物线解析式

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一家商店经营一种玩具,进价为每件50元,调查市场发现日销售量y(件)是关于售价x(元/件)的一次函数,相关数据如表,商店每天的总支出是600元.
售价(元/件) | 50 | 55 | 60 | 65 |
日销售量y/件 | 80 | 70 | 60 | 50 |
(1)直接写出y与x之间的函数关系式.(不要求写出自变量x的取值范围)
(2)商店在“五一”这天尽可能优惠顾客,正好收支平衡(收入=支出),问当天玩具的售价为多少元/件.
(3)商店最早需要多少天,纯利可以突破万元,玩具的售价应定为多少元/件?(每天纯利=每天的销售额﹣成本﹣每天的支出)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com