
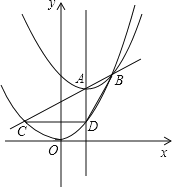
【题目】A是直线x=1上一个动点,以A为顶点的抛物线y1=a(x﹣1)2+t和抛物线y2=ax2交于点B(A,B不重合,a是常数),直线AB和抛物线y2=ax2交于点B,C,直线x=1和抛物线y2=ax2交于点D.(如图仅供参考)
(1)求点B的坐标(用含有a,t的式子表示);
(2)若a<0,且点A向上移动时,点B也向上移动,求![]() 的范围;
的范围;
(3)当B,C重合时,求![]() 的值;
的值;
(4)当a>0,且△BCD的面积恰好为3a时,求![]() 的值.
的值.
【答案】(1) 点B坐标为(![]() ,
,![]() );(2)
);(2)![]() >﹣1 ;(3)
>﹣1 ;(3) ![]() =﹣3;(4)
=﹣3;(4) ![]() 的值为﹣5或3
的值为﹣5或3
【解析】
(1)把两抛物解析式联立方程组,求得的解(含a、t的式子)即为点B坐标.
(2)由于A向上移动时,点B也向上移动,即点B纵坐标的值随点A纵坐标的值变大而变大,所以yB=![]() 随着t的增大而增大,把yB看作关于t的二次函数,可知当a<0时开口向下,故在对称轴左侧即t<a,yB随着t的增大而增大,利用不等式性质即求得
随着t的增大而增大,把yB看作关于t的二次函数,可知当a<0时开口向下,故在对称轴左侧即t<a,yB随着t的增大而增大,利用不等式性质即求得![]() ≥1且
≥1且![]() ≠1.
≠1.
(3)以点A、B坐标用待定系数法求直线AB解析式,在把直线AB和抛物线y2联立方程组另一交点C的坐标.
(4)把x=1代入y2=ax2求得点D坐标,发现点C、D纵坐标相等,即CD∥x轴,CD=2,所以△BCD面积等于CD与点B到CD距离乘积的一半.又点B到CD距离即点B与点C纵坐标之差,需分类讨论再结合a<0计算.
解:(1)∵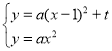 解得:
解得: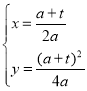
∴点B坐标为(![]() ,
,![]() )
)
(2)∵点A(1,t)向上移动,点B(![]() ,
,![]() )也向上移动
)也向上移动
∴yB=![]() 随着t的增大而增大
随着t的增大而增大
∵yB=![]() 可看作是yB关于t的二次函数
可看作是yB关于t的二次函数
∴当a<0时,此二次函数的图象开口向下,在t=﹣a时取得最大值为0
∴t<﹣a,yB随着t的增大而增大
∴![]() >﹣1
>﹣1
(3)设直线AB解析式为y=kx+b∴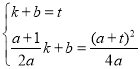 解得:
解得: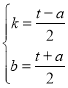
∴直线AB:y=![]() x+
x+![]()
∵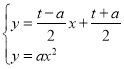 解得:
解得: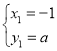
![]()
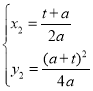 (即点B)
(即点B)
∴直线AB和抛物线y2=ax2另一交点C(﹣1,a)
∵B,C重合
∴![]()
∴a+t=﹣2a
∴3a=﹣t
∴![]() =﹣3
=﹣3
(4)∵直线x=1和抛物线y2=ax2交于点D
∴D(1,a)
∴CD∥x轴,CD=2
∴S△BCD=![]() CD|yB﹣yC|=|
CD|yB﹣yC|=|![]() ﹣a|=3a
﹣a|=3a
①当![]() ﹣a>0时,
﹣a>0时,![]() ﹣a=3a
﹣a=3a
整理得:15a2﹣2at﹣t2=0
∴(5a+t)(3a﹣t)=0
∴t=﹣5a或t=3a
∴![]() =﹣5或
=﹣5或![]() =3
=3
②当![]() ﹣a<0时,﹣
﹣a<0时,﹣![]() +a=3a
+a=3a
整理得:﹣(a+t)2=8a2
∵a>0
∴此式子不成立
综上所述,![]() 的值为﹣5或3.
的值为﹣5或3.



 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案科目:初中数学 来源: 题型:
【题目】(1)化简:(2x+1)(2x﹣1)+(x+1)(1﹣2x).
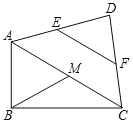
(2)如图,在四边形ABCD中,AB⊥BC,E,F,M分别是AD,DC,AC的中点,连接EF,BM,求证:EF=BM.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+3的图象与反比例函数![]() 的图象交于P、Q两点,PA⊥x轴于点A,一次函数的图象分别交x轴、y轴于点C、点B,其中OA=6,且
的图象交于P、Q两点,PA⊥x轴于点A,一次函数的图象分别交x轴、y轴于点C、点B,其中OA=6,且![]() .
.
(1)求一次函数和反比例函数的表达式;
(2)求△APQ的面积;
(3)根据图象写出当x取何值时,一次函数的值小于反比例函数的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
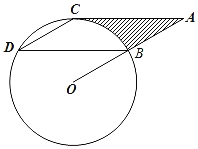
【题目】如图,点B、C、D都在⊙O上,过点C作AC∥BD交OB的延长线于点A,连接CD,且∠CDB=∠OBD=30°,BD=6![]() cm.
cm.
(1)求证:AC是⊙O的切线.
(2)求⊙O的半径长.
(3)求图中阴影部分的面积(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
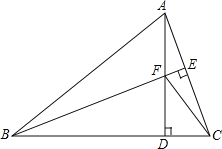
【题目】如图,在△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,∠BAD=45°,CD=![]() ,AD与BE交于点F,连接CF,则AD的长为_____.
,AD与BE交于点F,连接CF,则AD的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,AB为半圆的直径,O为圆心,C为圆弧上一点,AD垂直于过C点的切线,垂足为D,AB的延长线交直线CD于点E.
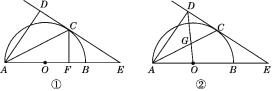
(1)求证:AC平分∠DAB;
(2)若AB=6,B为OE的中点,CF⊥AB,垂足为点F,求CF的长;
(3)如图②,连接OD交AC于点G,若![]() =
=![]() ,求cosE的值.
,求cosE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一座现代化大型单塔双面扇形斜拉桥,主桥采用独塔双面索斜拉设计,主桥桩呈“H”形,两侧用钢丝绳斜拉固定.
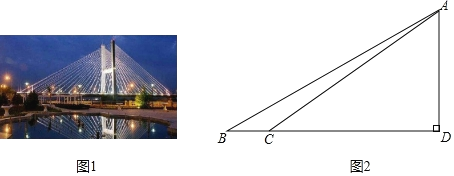
问题提出:
如何测量主桥桩顶端至桥面的距离AD?
方案设计:
如图,某数学课题研究小组通过调查研究和实地测量,在桥面B处测得∠ABC=26.57°,再沿BD方向走21米至C处,在C处测得∠ACD=30.96°.
问题解决:
根据上述方案和数据,求银滩黄河大桥主桥桩顶端至桥面的距离AD.
(结果精确到1m,参考数据:sin26.57°≈0.447,cos26.57°≈0.894,tan26.57°≈0.500,sin30.96°≈0.514,cos30.96°≈0.858,tan30.96°≈0.600)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】快慢两车分别从相距![]() 千米的甲、乙两地同时出发,匀速行驶,途中慢车因故障停留
千米的甲、乙两地同时出发,匀速行驶,途中慢车因故障停留![]() 小时,然后 以原速度的
小时,然后 以原速度的![]() 倍继续向甲地行驶,到达甲地后停止行驶;快车匀速到达乙地后,立即按原路原速返回甲 地(快车掉头时间忽略不计),并且比慢车提前
倍继续向甲地行驶,到达甲地后停止行驶;快车匀速到达乙地后,立即按原路原速返回甲 地(快车掉头时间忽略不计),并且比慢车提前![]() 分钟到达甲地,快慢两车之间的距离
分钟到达甲地,快慢两车之间的距离![]() (千米)与快 车行驶时间
(千米)与快 车行驶时间![]() (小时)之间的函数图象如图所示.则当两车第二次相遇时,两车距甲地还有________千米.
(小时)之间的函数图象如图所示.则当两车第二次相遇时,两车距甲地还有________千米.
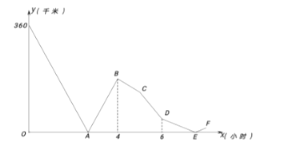
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c的顶点为D,与x轴交点A,B的横坐标分别为﹣1,3,与y轴负半轴交于点C.下面五个结论:
①2a+b=0;
②4a+2b+c>0;
③对任意实数x,ax2+bx≥a+b;
④只有当a=![]() 时,△ABD是等腰直角三角形;
时,△ABD是等腰直角三角形;
⑤使△ABC为等腰三角形的a值可以有3个.
其中正确的结论有_____.(填序号)
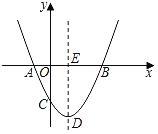
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com