
【题目】快慢两车分别从相距![]() 千米的甲、乙两地同时出发,匀速行驶,途中慢车因故障停留
千米的甲、乙两地同时出发,匀速行驶,途中慢车因故障停留![]() 小时,然后 以原速度的
小时,然后 以原速度的![]() 倍继续向甲地行驶,到达甲地后停止行驶;快车匀速到达乙地后,立即按原路原速返回甲 地(快车掉头时间忽略不计),并且比慢车提前
倍继续向甲地行驶,到达甲地后停止行驶;快车匀速到达乙地后,立即按原路原速返回甲 地(快车掉头时间忽略不计),并且比慢车提前![]() 分钟到达甲地,快慢两车之间的距离
分钟到达甲地,快慢两车之间的距离![]() (千米)与快 车行驶时间
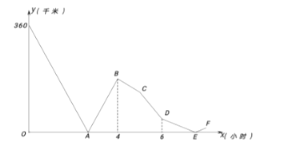
(千米)与快 车行驶时间![]() (小时)之间的函数图象如图所示.则当两车第二次相遇时,两车距甲地还有________千米.
(小时)之间的函数图象如图所示.则当两车第二次相遇时,两车距甲地还有________千米.
【答案】![]()
【解析】
由图象可知:快车4小时到乙地,6小时后慢车的速度是原速度的![]() ,5小时到6小时,慢车因故障停留
,5小时到6小时,慢车因故障停留![]() 小时,从而求出快车的速度和快车返回甲地的时间,设慢车原来的速度为x千米/小时,根据题意列出方程即可求出x,然后设t小时后,两车第二次相遇,利用此时快车比慢车多行驶360千米即可求出t,从而求出结论.
小时,从而求出快车的速度和快车返回甲地的时间,设慢车原来的速度为x千米/小时,根据题意列出方程即可求出x,然后设t小时后,两车第二次相遇,利用此时快车比慢车多行驶360千米即可求出t,从而求出结论.
解:由图象可知:快车4小时到乙地,6小时后慢车的速度是原速度的![]() ,5小时到6小时,慢车因故障停留
,5小时到6小时,慢车因故障停留![]() 小时,
小时,
∴快车的速度为360÷4=90千米/小时,快车4×2=8小时回到甲地
设慢车原来的速度为x千米/小时,则变速后的速度为![]() x千米/小时
x千米/小时
由题意可知5x+(8-6+![]() )×
)×![]() x=360
x=360
解得:x=45
设t小时后,两车第二次相遇
由题意可得90t=5×45+![]() ×45×(t-6)+360
×45×(t-6)+360
解得:t=![]()
∴当两车第二次相遇时,两车距甲地还有360×2-![]() ×90=45千米
×90=45千米
故答案为:45.


科目:初中数学 来源: 题型:
【题目】以下说法正确的是( )
A.小明做了![]() 次掷图钉的实验,发现
次掷图钉的实验,发现![]() 次钉尖朝上,由此他说钉尖朝上的概率是
次钉尖朝上,由此他说钉尖朝上的概率是![]()
B.一组对边平行,另一组对边相等的四边形是平行四边形
C.点![]() 都在反比例函数
都在反比例函数![]() 图象上,且
图象上,且![]() 则
则![]() ;
;
D.对于一元二元方程![]() ,若
,若![]() 则方程的两个根互为相反数
则方程的两个根互为相反数
查看答案和解析>>
科目:初中数学 来源: 题型:
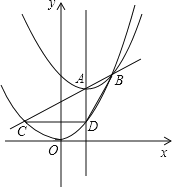
【题目】A是直线x=1上一个动点,以A为顶点的抛物线y1=a(x﹣1)2+t和抛物线y2=ax2交于点B(A,B不重合,a是常数),直线AB和抛物线y2=ax2交于点B,C,直线x=1和抛物线y2=ax2交于点D.(如图仅供参考)
(1)求点B的坐标(用含有a,t的式子表示);
(2)若a<0,且点A向上移动时,点B也向上移动,求![]() 的范围;
的范围;
(3)当B,C重合时,求![]() 的值;
的值;
(4)当a>0,且△BCD的面积恰好为3a时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=mx2+(1﹣2m)x+1﹣3m.
(1)当m=2时,求二次函数图象的顶点坐标;
(2)已知抛物线与x轴交于不同的点A、B.
①求m的取值范围;
②若3≤m≤4时,求线段AB的最大值及此时二次函数的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
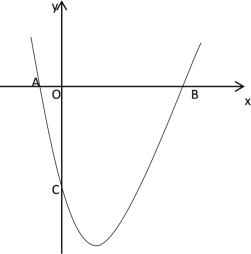
【题目】如图:已知抛物线![]() 与
与![]() 轴,
轴,![]() 轴分别交于点
轴分别交于点![]() ,此抛物线的对称轴为直线
,此抛物线的对称轴为直线![]() .
.
![]() 求出此抛物线的解析式;
求出此抛物线的解析式;
![]() 如图 1,抛物线的顶点为点
如图 1,抛物线的顶点为点![]() ,点
,点![]() 是直线
是直线![]() 下方抛物线上的一点(异于点
下方抛物线上的一点(异于点![]() ),当
),当![]() 时,求出点
时,求出点![]() 的坐标;
的坐标;
![]() 在
在![]() 的条件下,将抛物线沿射线
的条件下,将抛物线沿射线![]() 方向平移,点
方向平移,点![]() 的对应点为
的对应点为![]() ,在抛物线平移的过程中,若
,在抛物线平移的过程中,若![]() ,请直接写出此时平移后的抛物线解析式
,请直接写出此时平移后的抛物线解析式

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个批发商销售成本为20元/千克的某产品,根据物价部门规定:该产品每千克售价不得超过90元,在销售过程中发现的售量y(千克)与售价x(元/千克)满足一次函数关系,对应关系如下表:
售价x(元/千克) | … | 50 | 60 | 70 | 80 | … |
销售量y(千克) | … | 100 | 90 | 80 | 70 | … |
(1)求y与x的函数关系式;
(2)该批发商若想获得4000元的利润,应将售价定为多少元?
(3)该产品每千克售价为多少元时,批发商获得的利润w(元)最大?此时的最大利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
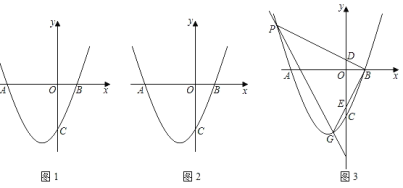
【题目】如图1,该抛物线是由y=x2平移后得到,它的顶点坐标为(﹣![]() ,﹣
,﹣![]() ),并与坐标轴分别交于A,B,C三点.
),并与坐标轴分别交于A,B,C三点.
(1)求A,B的坐标.
(2)如图2,连接BC,AC,在第三象限的抛物线上有一点P,使∠PCA=∠BCO,求点P的坐标.
(3)如图3,直线y=ax+b(b<0)与该抛物线分别交于P,G两点,连接BP,BG分别交y轴于点D,E.若ODOE=3,请探索a与b的数量关系.并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(1,a),B(m,n)(m>1)均在正比例函数y=2x的图象上,反比例函数y=![]() 的图象经过点A,过点B作BD⊥x轴于D,交反比例函数y=
的图象经过点A,过点B作BD⊥x轴于D,交反比例函数y=![]() 的图象于点C,连接AC,则下列结论正确的是( )
的图象于点C,连接AC,则下列结论正确的是( )
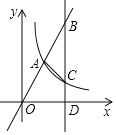
A.当m=2时,AC⊥OB
B.当AB=2OA时,BC=2CD
C.存在一个m,使得S△BOD=3S△OCD
D.四边形AODC的面积固定不变
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com