
����Ŀ����ͼ��һ���ִ������͵���˫������б���ţ����Ų��ö���˫����б����ƣ������ʡ�H���Σ������ø�˿��б���̶���
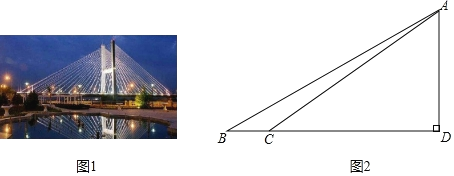
���������
��β�����������������ľ���AD��
������ƣ�
��ͼ��ij��ѧ�����о�С��ͨ�������о���ʵ�ز�����������B����á�ABC=26.57�㣬����BD������21����C������C����á�ACD=30.96�㣮
��������
�����������������ݣ�����̲�ƺӴ�����������������ľ���AD��
(�����ȷ��1m���ο����ݣ�sin26.57���0.447��cos26.57���0.894��tan26.57���0.500��sin30.96���0.514��cos30.96���0.858��tan30.96���0.600)
���𰸡���̲�ƺӴ�����������������ľ���ADΪ63�ף�
��������
�ȸ�������ó���ABD����ACD�Ķ�����BC�ij���������������Ǻ����Ķ��壬��Rt��ABD����AD��ʾBD����Rt��ACD����AD��ʾCD�������BD-CD=BC�г�AD�ķ��̣����AD��ɣ�
�⣺��������ã�
��ABD=26.57�㣬��ACD=30.96�㣬BC=21�ף�
��Rt��ABD�У���ABD=26.57�㣬
��tan��ABD![]() ��
��
��BD![]() ��
��
��Rt��ACD�У���ACD=30.96�㣬
��tan��ACD![]() ��
��
��CD![]() ��
��
��BD��CD=BC��BC=21��
��2AD![]() ��
��
��AD=63(��)��
����̲�ƺӴ�����������������ľ���ADΪ63�ף�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����ר��һ��綯��ˢ����ɱ�Ϊ20Ԫ/֧�������з��֣�����Ʒÿ���������y(֧�������۵���x(Ԫ/֧��֮�������ͼ��ʾ�Ĺ�ϵ��
(1)��y��x֮��ĺ�����ϵʽ��
(2)���ں���ʡ�人�б���������״�������ף�������¹ڷ����������飬���������������ÿ���õ������г��200Ԫ�����人��Ϊ�˱�֤����ÿ��ʣ��������550Ԫ�����ȷ�����綯��ˢ�����۵��ۣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ƻ�����ʩ������������ò����������Ʒ�ʹ����У�2019�����п�չ���е����칤�̣���Ҫ�����ҵذ�ש�������е��������üס������ֻ������صذ�ש����֪һ���׳�ÿ�����ص�������һ���ҳ���2�֣��Ҽ׳�����16�ֵذ�ש���ҳ�����12�ֵذ�ש���õij�������ͬ��
��1���ס������ֻ���ÿ�����صذ�ש�����ٶ֣�
��2�������ü׳�a�����ҳ�b�����պ����صذ�ש100�֣���a��3b�����ж������������
��3���ڣ�2������֪һ���׳�ÿ�ε��˷���380Ԫ��һ���ҳ�ÿ�ε��˷���300Ԫ��������üס������ֳ���ʹ�����˷���ͣ����������˷ѣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��A��ֱ��x=1��һ�����㣬��AΪ�����������y1=a(x��1)2+t��������y2=ax2���ڵ�B(A��B���غϣ�a�dz���)��ֱ��AB��������y2=ax2���ڵ�B��C��ֱ��x=1��������y2=ax2���ڵ�D��(��ͼ�����ο�)
(1)���B������(�ú���a��t��ʽ�ӱ�ʾ)��
(2)��a��0���ҵ�A�����ƶ�ʱ����BҲ�����ƶ�����![]() �ķ�Χ��
�ķ�Χ��
(3)��B��C�غ�ʱ����![]() ��ֵ��
��ֵ��
(4)��a��0���ҡ�BCD�����ǡ��Ϊ3aʱ����![]() ��ֵ��
��ֵ��
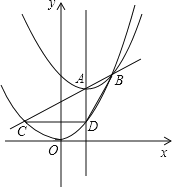
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������龳��
���ۺ���ʵ�����ϣ���ʦ��ͬѧ���ԡ�����ֽƬ�ļ�ƴ��Ϊ���չ��ѧ����� ͼ 1����������ֽƬ ABCD �ضԽ��� AC �������õ���ABC �͡�ACD���������� AB ��4cm��AC��8cm��
�������֣�
��1����ͼ 1 �еġ�ACD �Ե� A Ϊ��ת���ģ�����ʱ�뷽����ת�Ϧ���ʹ�Ϧ�����BAC���õ���ͼ 2 ��ʾ�ġ�AC��D������ C �� AC���ƽ���ߣ��� DC'���ӳ��� ���ڵ� E�����ı��� ACEC�����״�� ��
��2������С�齫ͼ 1 �еġ�ACD �Ե� A Ϊ��ת���ģ�����ʱ�뷽����ת��ʹ B�� A��D ������ͬһ��ֱ���ϣ��õ���ͼ 3 ��ʾ�ġ�AC��D������ CC'��ȡ CC����� �� F������ AF ���ӳ����� G��ʹ FG��AF������ CG��C��G���õ��ı��� ACGC�䣬 �������������Σ�����֤��������ۣ�
ʵ��̽����
��3������С���ڴ���С�鷢�ֽ��۵Ļ����ϣ��������²���������ABC ���� BD ����ƽ�ƣ�ʹ�� B ��� A �غϣ���ʱ A ��ƽ���� A'�㣬A'C �� BC���ཻ�ڵ� H�� ��ͼ 4 ��ʾ������ CC�䣬���� tan��C��CH ��ֵ��
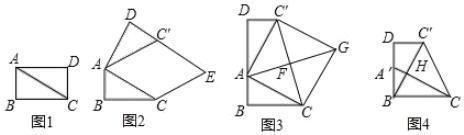
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() �ǵȱ������Σ���һ�������أ�
�ǵȱ������Σ���һ�������أ�![]() ���س����ȷ֣�EH��BC�����ı���
���س����ȷ֣�EH��BC�����ı���![]() �������
�������![]() ������ģ�( )
������ģ�( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=mx2+(1��2m)x+1��3m��
(1)��m=2ʱ������κ���ͼ��Ķ������ꣻ
(2)��֪��������x�ύ�ڲ�ͬ�ĵ�A��B��
����m��ȡֵ��Χ��
����3��m��4ʱ�����߶�AB�����ֵ����ʱ���κ����ı���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�����������۳ɱ�Ϊ20Ԫ/ǧ�˵�ij��Ʒ��������۲��Ź涨���ò�Ʒÿǧ���ۼ۲��ó���90Ԫ�������۹����з��ֵ�����y��ǧ�ˣ����ۼ�x��Ԫ/ǧ�ˣ�����һ�κ�����ϵ����Ӧ��ϵ���±���
�ۼ�x��Ԫ/ǧ�ˣ� | �� | 50 | 60 | 70 | 80 | �� |
������y��ǧ�ˣ� | �� | 100 | 90 | 80 | 70 | �� |
��1����y��x�ĺ�����ϵʽ��
��2����������������4000Ԫ������Ӧ���ۼ۶�Ϊ����Ԫ��
��3���ò�Ʒÿǧ���ۼ�Ϊ����Ԫʱ�������̻�õ�����w��Ԫ�����ʱ���������Ϊ����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ϴ�»���ϴ���·�ʱ�������˽�ˮ����ϴ����ˮ����ˮ�ĸ������Ĺ��̣����н�ˮ����ϴ����ˮʱϴ�»��е�ˮ��y��������ʱ��x�����ӣ�֮��Ĺ�ϵ��ͼ��ʾ����֪��ϴ�»�����ˮ�ٶ�Ϊÿ����20����
��1������ˮʱy��x֮��ĺ�������ʽ��
��2��ϴ�»��е�ˮ������ijһˮλ��13.7�����ֵ����ˮλ�����ˮλΪ��������
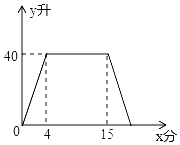
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com