
【题目】如图,抛物线y=ax2+bx+c的顶点为D,与x轴交点A,B的横坐标分别为﹣1,3,与y轴负半轴交于点C.下面五个结论:
①2a+b=0;
②4a+2b+c>0;
③对任意实数x,ax2+bx≥a+b;
④只有当a=![]() 时,△ABD是等腰直角三角形;
时,△ABD是等腰直角三角形;
⑤使△ABC为等腰三角形的a值可以有3个.
其中正确的结论有_____.(填序号)
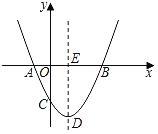
【答案】①③④.
【解析】
先根据图象与x轴的交点A,B的横坐标分别为﹣1,3确定出AB的长及对称轴,再由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
解:①∵图象与x轴的交点A,B的横坐标分别为﹣1,3,
∴AB=4,
∴对称轴x=﹣![]() =1,
=1,
即2a+b=0;
故①正确,符合题意;
②由图象看,当x=2时,y=4a+2b+c<0,
故②错误,不符合题意;
③函数的对称轴为直线x=1,函数在x=1时,取得最小值,
故ax2+bx+c≥a+b+c,
即ax2+bx≥a+b正确,符合题意;
④要使△ABD为等腰直角三角形,必须保证D到x轴的距离等于AB长的一半;
D到x轴的距离就是当x=1时y的值的绝对值.
当x=1时,y=a+b+c,
即|a+b+c|=2,
∵当x=1时,y<0,
∴a+b+c=﹣2,
又∵图象与x轴的交点A,B的横坐标分别为﹣1,3,
∴当x=﹣1时y=0,即a﹣b+c=0;
当x=3时,y=0.
∴9a+3b+c=0,
解这三个方程可得:b=﹣1,a=![]() ,c=﹣
,c=﹣![]() ,
,
故④正确,符合题意;
⑤要使△ACB为等腰三角形,则必须保证AB=BC=4或AB=AC=4或AC=BC,
当AB=BC=4时,
∵AO=1,△BOC为直角三角形,
又∵OC的长即为|c|,
∴c2=16﹣9=7,
∵由抛物线与y轴的交点在y轴的负半轴上,
∴c=﹣![]() ,
,
与2a+b=0、a﹣b+c=0联立组成解方程组,解得a=![]() ;
;
同理当AB=AC=4时,
∵AO=1,△AOC为直角三角形,
又∵OC的长即为|c|,
∴c2=16﹣1=15,
∵由抛物线与y轴的交点在y轴的负半轴上,
∴c=﹣![]() ,
,
与2a+b=0、a﹣b+c=0联立组成解方程组,解得a=![]() ;
;
同理当AC=BC时
在△AOC中,AC2=1+c2,
在△BOC中BC2=c2+9,
∵AC=BC,
∴1+c2=c2+9,此方程无解.
经解方程组可知只有两个a值满足条件.
故⑤错误.
故答案为:①③④.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
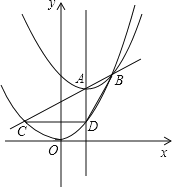
【题目】A是直线x=1上一个动点,以A为顶点的抛物线y1=a(x﹣1)2+t和抛物线y2=ax2交于点B(A,B不重合,a是常数),直线AB和抛物线y2=ax2交于点B,C,直线x=1和抛物线y2=ax2交于点D.(如图仅供参考)
(1)求点B的坐标(用含有a,t的式子表示);
(2)若a<0,且点A向上移动时,点B也向上移动,求![]() 的范围;
的范围;
(3)当B,C重合时,求![]() 的值;
的值;
(4)当a>0,且△BCD的面积恰好为3a时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个批发商销售成本为20元/千克的某产品,根据物价部门规定:该产品每千克售价不得超过90元,在销售过程中发现的售量y(千克)与售价x(元/千克)满足一次函数关系,对应关系如下表:
售价x(元/千克) | … | 50 | 60 | 70 | 80 | … |
销售量y(千克) | … | 100 | 90 | 80 | 70 | … |
(1)求y与x的函数关系式;
(2)该批发商若想获得4000元的利润,应将售价定为多少元?
(3)该产品每千克售价为多少元时,批发商获得的利润w(元)最大?此时的最大利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
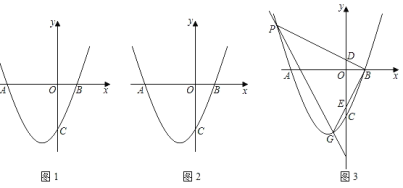
【题目】如图1,该抛物线是由y=x2平移后得到,它的顶点坐标为(﹣![]() ,﹣
,﹣![]() ),并与坐标轴分别交于A,B,C三点.
),并与坐标轴分别交于A,B,C三点.
(1)求A,B的坐标.
(2)如图2,连接BC,AC,在第三象限的抛物线上有一点P,使∠PCA=∠BCO,求点P的坐标.
(3)如图3,直线y=ax+b(b<0)与该抛物线分别交于P,G两点,连接BP,BG分别交y轴于点D,E.若ODOE=3,请探索a与b的数量关系.并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
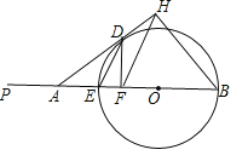
【题目】已知,如图,EB是![]() 的直径,且
的直径,且![]() ,在BE的延长线上取点P,使
,在BE的延长线上取点P,使![]() ,A是EP上一点,过A作
,A是EP上一点,过A作![]() 的切线,切点为D,过D作
的切线,切点为D,过D作![]() 于F,过B作AD的垂线BH,交AD的延长线于
于F,过B作AD的垂线BH,交AD的延长线于![]() 当点A在EP上运动,不与E重合时:
当点A在EP上运动,不与E重合时:
![]() 是否总有
是否总有![]() ,试证明你的结论;
,试证明你的结论;
![]() 设
设![]() ,
,![]() ,求y和x的函数关系,并写出x的取值范围.
,求y和x的函数关系,并写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一家商店经营一种玩具,进价为每件50元,调查市场发现日销售量y(件)是关于售价x(元/件)的一次函数,相关数据如表,商店每天的总支出是600元.
售价(元/件) | 50 | 55 | 60 | 65 |
日销售量y/件 | 80 | 70 | 60 | 50 |
(1)直接写出y与x之间的函数关系式.(不要求写出自变量x的取值范围)
(2)商店在“五一”这天尽可能优惠顾客,正好收支平衡(收入=支出),问当天玩具的售价为多少元/件.
(3)商店最早需要多少天,纯利可以突破万元,玩具的售价应定为多少元/件?(每天纯利=每天的销售额﹣成本﹣每天的支出)
查看答案和解析>>
科目:初中数学 来源: 题型:
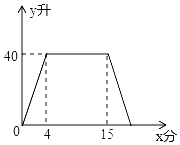
【题目】某种洗衣机在洗涤衣服时,经历了进水、清洗、排水、脱水四个连续的过程,其中进水、清洗、排水时洗衣机中的水量y(升)与时间x(分钟)之间的关系如图所示.已知:洗衣机的排水速度为每分钟20升.
(1)求排水时y与x之间的函数解析式;
(2)洗衣机中的水量到达某一水位后,过13.7分钟又到达该水位,求该水位为多少升.
查看答案和解析>>
科目:初中数学 来源: 题型:
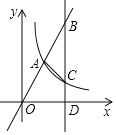
【题目】已知点A(1,a),B(m,n)(m>1)均在正比例函数y=2x的图象上,反比例函数y=![]() 的图象经过点A,过点B作BD⊥x轴于D,交反比例函数y=
的图象经过点A,过点B作BD⊥x轴于D,交反比例函数y=![]() 的图象于点C,连接AC,则下列结论正确的是( )
的图象于点C,连接AC,则下列结论正确的是( )
A.当m=2时,AC⊥OB
B.当AB=2OA时,BC=2CD
C.存在一个m,使得S△BOD=3S△OCD
D.四边形AODC的面积固定不变
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 过点
过点![]() ,且与直线
,且与直线![]() 交于B、C两点,点B的坐标为
交于B、C两点,点B的坐标为![]() .
.
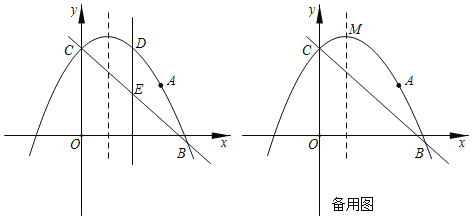
(1)求抛物线的解析式;
(2)点D为抛物线上位于直线![]() 上方的一点,过点D作
上方的一点,过点D作![]() 轴交直线
轴交直线![]() 于点E,点P为对称轴上一动点,当线段
于点E,点P为对称轴上一动点,当线段![]() 的长度最大时,求
的长度最大时,求![]() 的最小值;
的最小值;
(3)设点M为抛物线的顶点,在y轴上是否存在点Q,使![]() ?若存在,求点Q的坐标;若不存在,请说明理由.
?若存在,求点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com