
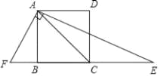
【题目】如图,正方形ABCD边长为1,连接AC,AE平分∠CAD,交BC的延长线于点E,FA⊥AE,交CE于点F,则EF的长为____.
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:初中数学 来源: 题型:
【题目】定义:给定两个不等式组![]() 和
和![]() ,若不等式组
,若不等式组![]() 的任意一个解,都是不等式组
的任意一个解,都是不等式组![]() 的一个解,则称不等式组
的一个解,则称不等式组![]() 为不等式组
为不等式组![]() 的“子集”例如:不等式组:
的“子集”例如:不等式组:![]() 是:
是:![]() 的“子集”.
的“子集”.
(1)若不等式组:![]() ,
,![]() ,其中不等式组_________是不等式组
,其中不等式组_________是不等式组![]() 的“子集”(填
的“子集”(填![]() 或
或![]() );
);
(2)若关于![]() 的不等式组
的不等式组![]() 是不等式组
是不等式组![]() 的“子集”,则
的“子集”,则![]() 的取值范围是________;
的取值范围是________;
(3)已知![]() 为互不相等的整数,其中
为互不相等的整数,其中![]() ,
,![]() ,下列三个不等式组:
,下列三个不等式组:![]() ,
,![]() ,
,![]() 满足:
满足:![]() 是
是![]() 的“子集”且
的“子集”且![]() 是
是![]() 的“子集”,则
的“子集”,则![]() 的值为__________;
的值为__________;
(4)已知不等式组![]() 有解,且
有解,且![]() 是不等式组
是不等式组![]() 的“子集”,请写出
的“子集”,请写出![]() ,
,![]() 满足的条件:________________.
满足的条件:________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将正方形对折后展开(图④是连续两次对折后再展开),再按图示方法折叠,能够得到一个直角三角形(阴影部分),且它的一条直角边等于斜边的一半,这样的图形有( ).

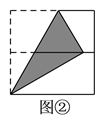


A. ![]() 个 B.
个 B. ![]() 个 C.
个 C. ![]() 个 D.
个 D. ![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O的半径为2,AB为直径,CD为弦.AB与CD交于点M,将 ![]() 沿CD翻折后,点A与圆心O重合,延长OA至P,使AP=OA,连接PC
沿CD翻折后,点A与圆心O重合,延长OA至P,使AP=OA,连接PC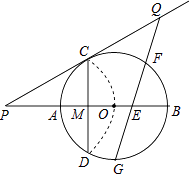
(1)求CD的长;
(2)求证:PC是⊙O的切线;
(3)点G为 ![]() 的中点,在PC延长线上有一动点Q,连接QG交AB于点E.交
的中点,在PC延长线上有一动点Q,连接QG交AB于点E.交 ![]() 于点F(F与B、C不重合).问GEGF是否为定值?如果是,求出该定值;如果不是,请说明理由.
于点F(F与B、C不重合).问GEGF是否为定值?如果是,求出该定值;如果不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是边长为a的正方形,点G,E分别是边AB,BC的中点,∠AEF=90°,且EF交正方形外角的平分线CF于点F.
(1)证明:∠BAE=∠FEC;
(2)证明:△AGE≌△ECF;
(3)求△AEF的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,BC=3,AC= ![]() ,AB的垂直平分线ED交BC的延长线于D点,垂足为E,则sin∠CAD=( )
,AB的垂直平分线ED交BC的延长线于D点,垂足为E,则sin∠CAD=( )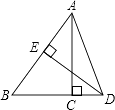
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,∠A,∠B,∠C的对边分别为a、b、c,下列说法中错误的是( )
A.如果∠C-∠B=∠A,则△ABC是直角三角形,且∠C=90;
B.如果![]() ,则△ABC是直角三角形,且∠C=90;
,则△ABC是直角三角形,且∠C=90;
C.如果(c+a)( c-a)=![]() ,则△ABC是直角三角形,且∠C=90;
,则△ABC是直角三角形,且∠C=90;
D.如果∠A:∠B:∠C=3:2:5,则△ABC是直角三角形,且∠C=90.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1为深50cm的圆柱形容器,底部放入一个长方体的铁块,现在以一定的速度向容器内注水,图2为容器顶部离水面的距离y(cm)随时间t(分钟)的变化图象,则( )
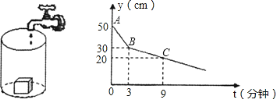
A. 注水的速度为每分钟注入![]() cm高水位的水
cm高水位的水
B. 放人的长方体的高度为30cm
C. 该容器注满水所用的时间为21分钟
D. 此长方体的体积为此容器的体积的0.35.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com