
 �ο��Ͻ��ɽ�����ַ�ʽ��һ���Ǵ�������ɽ����ͼ���ȴ�A�ص�ɽ�����ߵ�B���������������³���C����һ���Ǵӱ��¾���������ɽ��·������ɽ��C����֪��A���۲�C�������ǡ�CAD=31�㣬��A��B��ˮƽ����AE=1500�ף�A��B����ֱ����BE=750�ף�����BC�¶�i=2��3��CD��AD��D��BF��CD��F��
�ο��Ͻ��ɽ�����ַ�ʽ��һ���Ǵ�������ɽ����ͼ���ȴ�A�ص�ɽ�����ߵ�B���������������³���C����һ���Ǵӱ��¾���������ɽ��·������ɽ��C����֪��A���۲�C�������ǡ�CAD=31�㣬��A��B��ˮƽ����AE=1500�ף�A��B����ֱ����BE=750�ף�����BC�¶�i=2��3��CD��AD��D��BF��CD��F������ ��1���������⣬������CF=2x����BF=3x��Ȼ�����������Ǻ���ֵ�������������x��ֵ���Ӷ������������BC�ij���
��2��������֪����������֪���������˵��ٶ�֮��Ĺ�ϵ������������Ǻ���ֵ���ٶȵ���·�̳���ʱ�䣬�������Խ���⣮
��� �⣺��1����CF=2x����BF=3x��
��tan31���0.6��tan31��=$\frac{2x+750}{1500+3x}$��
��$\frac{2x+750}{1500+3x}=0.6$
��ã�x=750��
�����飬x=750��ԭ��ʽ���̵Ľ⣬
��BF=2250��CF=1500��
��BC=$\sqrt{B{F}^{2}+C{F}^{2}}=\sqrt{225{0}^{2}+150{0}^{2}}$=750$\sqrt{13}$�ף�
������BC�ij���$750\sqrt{13}$�ף�
��2������ص�ɽ�������е�ƽ���ٶ���m��/���ӣ�
$\frac{2100}{m}+\frac{750\sqrt{13}}{150}-\frac{20000}{8m}=10$��$\sqrt{13}��3.6$��
��ã�m=50��
�����飬m=50��ԭ��ʽ���̵Ľ⣬
�����ص�ɽ�������е�ƽ���ٶ���50��/���ӣ�
���� ���⿼���ֱ��������-�¶��½����⣬����Ĺؼ�����ȷ���⣬�ҳ�����������Ҫ��������


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��O���߶�AB��һ�㣬E��F�ֱ���AO��OB���е㣬��EF=3��AO=2����OB=4��
��ͼ��O���߶�AB��һ�㣬E��F�ֱ���AO��OB���е㣬��EF=3��AO=2����OB=4���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x��0 | B�� | x��0 | C�� | x��0��һ��ʵ�� | D�� | xȡ����ʵ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ����ABC�Ķ���A��B��C���ڡ�O�ϣ�����ABC+��AOC=90�㣬���ABC�Ĵ�С�ǣ�������
��ͼ����ABC�Ķ���A��B��C���ڡ�O�ϣ�����ABC+��AOC=90�㣬���ABC�Ĵ�С�ǣ�������| A�� | 30�� | B�� | 45�� | C�� | 60�� | D�� | 70�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
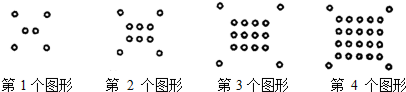
| A�� | 4n+��n+1�� | B�� | n2+4n | C�� | 4+n��n+1�� | D�� | 4+��n+1��2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ���ڡ�ABC�У���C=90�㣬AC=2��BC=1����cosA��ֵ�ǣ�������
��ͼ���ڡ�ABC�У���C=90�㣬AC=2��BC=1����cosA��ֵ�ǣ�������| A�� | $\frac{1}{2}$ | B�� | $\frac{\sqrt{5}}{2}$ | C�� | $\frac{\sqrt{5}}{5}$ | D�� | $\frac{2\sqrt{5}}{5}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{8}{9}$ | B�� | -8 | C�� | $\frac{2}{3}$ | D�� | 0 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com