
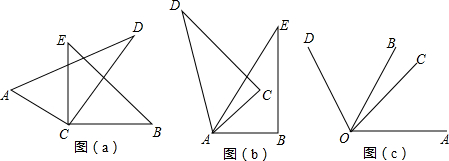
���� ��1���������BCD���ٴ����ACB=��ACD+��BCD������ɣ��������BCD���ٴ����DCE=��BCE-��BCD������ɣ�
��2�����ݡ�ACB=��ACE+��DCE+��DCE������ɣ�
��3�����ݡ�DAB=��DAE+��CAE+��CAB������ɣ�
��4�����ݡ�AOD=��AOC+��COB+��BOD������ɣ�
��� �⣺��1���ߡ�BCE=90�㣬��DCE=25�㣬
���BCD=��BCE-��DCE=65�㣬
�ߡ�ACD=90�㣬
���ACB=��ACD+��BCD=90��+65��=155�㣻
�ߡ�ACB=130�㣬��ACD=90�㣬
���BCD=��ACB-��ACD=130��-90��=40�㣬
�ߡ�BCE=90�㣬
���DCE=��BCE-��BCD=90��-40��=50�㣬
�ʴ�Ϊ��155�㣬50�㣻
��2����ACB+��DCE=180�㣬
�������£��ߡ�ACB=��ACE+��DCE+��DCE��
���ACB+��DCE
=��ACE+��DCE+��DCE+��DCE
=��ACD+��BCE
=180�㣻
��3����DAB+��CAE=120�㣬�������£�
�ߡ�DAB=��DAE+��CAE+��CAB��
���DAB+��CAE
=��DAE+��CAE+��CAB+��CAE
=��DAC+��BAE
=120�㣻
��4����AOD+��BOC=��+�£��������£�
�ߡ�AOD=��AOC+��COB+��BOD��
���AOD+��BOC
=��AOC+��COB+��BOD+��BOC
=��AOB+��COD
=��+�£�
���� ���⿼���˽ǵ��йؼ����Ӧ�ã���������ýǵĺͲ���м����ǽ����Ĺؼ������������ƣ�


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
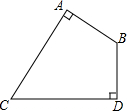 ��ͼ���ı���ABDC�У���ABD=120�㣬AB��AC��BD��CD��AB=4��CD=4$\sqrt{3}$������ı��ε������16$\sqrt{3}$��
��ͼ���ı���ABDC�У���ABD=120�㣬AB��AC��BD��CD��AB=4��CD=4$\sqrt{3}$������ı��ε������16$\sqrt{3}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ڡ�ABC�У�AB=AC����BAC=90�㣬DΪAC����һ�㣬����BD��AF��BD�ڵ�F����E��BF�ϣ�����AE����EAF=45�㣻
��ͼ���ڡ�ABC�У�AB=AC����BAC=90�㣬DΪAC����һ�㣬����BD��AF��BD�ڵ�F����E��BF�ϣ�����AE����EAF=45�㣻�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
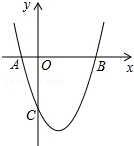 ��ͼ��������y=x2+bx+c��x�ύ��A��-1��0����B��3��0�����㣮
��ͼ��������y=x2+bx+c��x�ύ��A��-1��0����B��3��0�����㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x2+2x=x2-1 | B�� | ax2+bx+c=0 | C�� | 3��x+1��2=2��x+1�� | D�� | $\frac{1}{{x}^{2}}$+$\frac{1}{x}$-2=0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
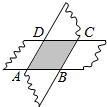 ��ͼ�������ŶԱ�ƽ�е�ֽ�������⽻�������һ��ת�����е�һ�ţ��غϵIJ��ֹ�����һ���ı��Σ�����ı�����ƽ���ı��Σ�
��ͼ�������ŶԱ�ƽ�е�ֽ�������⽻�������һ��ת�����е�һ�ţ��غϵIJ��ֹ�����һ���ı��Σ�����ı�����ƽ���ı��Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com