
【题目】小张去书店购买图书,看好书店有A,B,C三种不同价格的图书,分别是A种图书每本1元,B种图书每本2元,C种图书每本5元.
(1)若小张同时购买A,C两种不同图书的6本,用去18元,求购买两种图书的本数;
(2)若小张同时购买两种不同的图书10本,用去18元,请你设计他的购书方案;
(3)若小张同时购进A,B,C三种不同图书10本,用去18元,请你设计他的购买方案.
【答案】(1)小张购买A种图书3本,购买C种图书3本;(2)小张共有2种购书方案:方案一:购买A种图书2本,购买B种图书8本;方案二:购买A种图书8本,购买C种图书2本;(3)小张的购书方案为:购买A种图书5本,购买B种图书4本,购买C种图书1本.
【解析】
(1)设小张购买A种图书x本,则购买C种图书(6﹣x)本,根据购买A,C两种不同图书一共用去18元列出方程,求解即可;
(2)因为书店有A,B,C三种不同价格的图书,而小张同时购买两种不同的图书,所以要将A,B,C两两组合,分三种情况:A,B;A,C;B,C,每种情况都可以根据下面两个相等关系列出方程,两种不同价格的图书本数之和=10,购买两种不同价格的图书钱数之和=18,然后根据实际含义确定他们的解;
(3)有两个等量关系:A种图书本数+B种图书本数+C种图书本数=10,购买A种图书钱数+购买B种图书钱数+购买C种图书钱数=18.设两个未知数,得出二元一次方程,根据实际含义确定解.
(1)设小张购买A种图书x本,则购买C种图书(6﹣x)本.
根据题意,得x+5(6﹣x)=18,
解得x=3,
则6﹣x=3.
答:小张购买A种图书3本,购买C种图书3本;
(2)分三种情况讨论:
①设购买A种图书y本,则购买B种图书(10﹣y)本.
根据题意,得y+2(10﹣y)=18,
解得y=2,
则10﹣y=8;
②设购买A种图书y本,则购买C种图书(10﹣y)本.
根据题意,得y+5(10﹣y)=18,
解得y=8,
则10﹣y=2;
③设购买B种图书y本,则购买C种图书(10﹣y)本.
根据题意,得2y+5(10﹣y)=18,
解得y=![]() ,
,
则10﹣y=﹣![]() ,不合题意舍去.
,不合题意舍去.
综上所述,小张共有2种购书方案:
方案一:购买A种图书2本,购买B种图书8本;
方案二:购买A种图书8本,购买C种图书2本;
(3)设购买A种图书m本,购买B种图书n本,则购买C种图书(10﹣m﹣n)本.
根据题意,得m+2n+5(10﹣m﹣n)=18,
整理,得4m+3n=32,
∵m、n都是正整数,0<4m<32,
∴0<m<8,
将m=1,2,3,4,5,6,7分别代入,仅当m=5时,n为整数,n=4,
∴m=5,n=4,10﹣m﹣n=1.
答:小张的购书方案为:购买A种图书5本,购买B种图书4本,购买C种图书1本.


科目:初中数学 来源: 题型:
【题目】如图,一块长和宽分别为60厘米和40厘米的长方形铁皮,要在它的四角截去四个相等的小正方形,折成一个无盖的长方体水槽,使它的底面积为800平方厘米.求截去正方形的边长.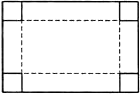
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小组做“用频率估计概率”的实验时,绘出的某一结果出现的频率折线图,则符合这一结果的实验可能是( )

A. 抛一枚硬币,出现正面朝上
B. 掷一个正六面体的骰子,出现3点朝上
C. 一副去掉大小王的扑克牌洗匀后,从中任抽一张牌的花色是红桃
D. 从一个装有2个红球1个黑球的袋子中任取一球,取到的是黑球
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为锐角三角形ABC的外心,四边形OCDE为正方形,其中E点在△ABC的外部,判断下列叙述何者正确( )
A.O是△AEB的外心,O是△AED的外心
B.O是△AEB的外心,O不是△AED的外心
C.O不是△AEB的外心,O是△AED的外心
D.O不是△AEB的外心,O不是△AED的外心
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,在斜边AB上分别截取AD=AC,BE=BC,DE=6,
点O是△CDE的外心,如图所示,则点O到△ABC的三边的距离之和是 . 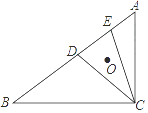
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一张矩形纸片ABCD沿EF折叠后,点A落在CD边上的点A′处,点B落在点B′处,若∠2=40°,则图中∠1的度数为( )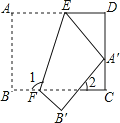
A.115°
B.120°
C.130°
D.140°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,∠MON=40°,OE平分∠MON,A,B,C分别是射线OM,OE,ON上的动点(A,B,C不与点O 重合),连接AC交射线OE于点D.设∠OAC=x°.
(1)如图①,若AB∥ON,则
①∠ABO的度数是________.
②当∠BAD=∠ABD时,x=________;当∠BAD=∠BDA时,x=________.
(2)如图②,若AB⊥OM,则是否存在这样的x值,使得△ADB中有两个相等的角?若存在,求出x的值;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,OE平分∠BOC,OF⊥OE,OP⊥CD,∠ABO=40°,则下列结论:①∠BOE=70°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正确结论有_____填序号)
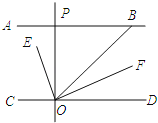
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,将一块含有45°角的直角三角板如图放置,直角顶点C的坐标为(1,0),顶点A的坐标为(0,2),顶点B恰好落在第一象限的双曲线上,现将直角三角板沿x轴正方向平移,当顶点A恰好落在该双曲线上时停止运动,则此时点C的对应点C′的坐标为( )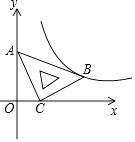
A.( ![]() ,0)
,0)
B.(2,0)
C.( ![]() ,0)
,0)
D.(3,0)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com