
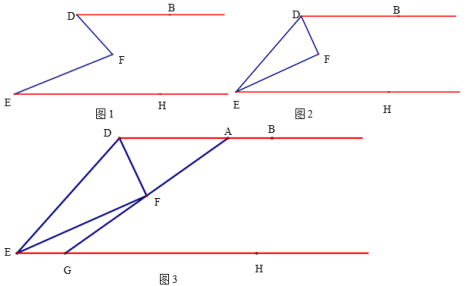
【题目】已知DB∥EH,F是两条射线内一点,连接DF、EF.
(1)如图1:求证:∠F=∠D+∠E;
(2)如图2:连接DE,∠BDE、∠HED的角平分交于点F时,求∠F的度数;
(3)在(2)条件下,点A是射线DB上任意一点,连接AF,并延长交EH于点G,求证:AF=FG.
【答案】(1)见解析;(2)![]() ;(3)见解析.
;(3)见解析.
【解析】
(1)过点F作FM∥BD,则FM∥HE,又根据FM∥BD,即可有∠1=∠D,∠2=∠E,则可证明∠F=∠D+∠E;(2)根据角平分线得出∠3=∠5,∠4=∠6,DB∥HE得出∠3+∠5+∠4+∠6=1800,即可证明∠F=900;(3)过F点作BD的垂线,垂足为K,延长KF交EH于点I;过F点作FJ垂线于点J,根据DA∥EH得出∠AKF=∠GIF=900,由角平分线得出KF=FJ,FI=FJ,所以KF=FI,则可证明△AKF≌△GIF,所以AF=FG.
(1)过点F作FM∥BD,则FM∥HE,

∵FM∥BD,FM∥HE
∴∠1=∠D,∠2=∠E
∵∠F=∠1+∠2
∴∠F=∠D+∠E
(2)
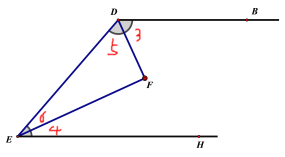
∵DF是角平分线
∴∠3=∠5
又∵EF是角平分线
∴∠4=∠6
又∵DB∥HE
∴∠3+∠5+∠4+∠6=1800
∴∠5+∠6=900
∴∠F=900
(3)过F点作BD的垂线,垂足为K,延长KF交EH于点I;过F点作FJ垂线于点J

∵DA∥EH
∴∠AKF=∠GIF=900
∵DF是角平分线
∴KF=FJ
EF是角平分线
∴FI=FJ
∴KF=FI
在△AKF和△GIF中

∴△AKF≌△GIF(AAS)
∴AF=FG


科目:初中数学 来源: 题型:
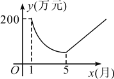
【题目】保护生态环境,建设绿色社会已经从理念变为人们的行动,某化工厂2014年1月的利润为200万元.设2014年1月为第1个月,第x个月的利润为y万元.由于排污超标,该厂决定从2014年1月底起适当限产,并投入资金进行治污改造,导致月利润明显下降,从1月到5月,y与x成反比例,到5月底,治污改造工程顺利完工,从这时起,该厂每月的利润比前一个月增加20万元(如图).
(1)分别求该化工厂治污期间及治污改造工程完工后,y与x之间的函数关系式;
(2)治污改造工程顺利完工后经过几个月,该厂月利润才能达到200万元?
(3)当月利润少于100万元时,为该厂资金紧张期,问该厂资金紧张期共有几个月?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt![]() 中,
中,![]() ,AB=BC,F为AB上一点,连接CF,过B作BH⊥CF于G,交AC于H.
,AB=BC,F为AB上一点,连接CF,过B作BH⊥CF于G,交AC于H.
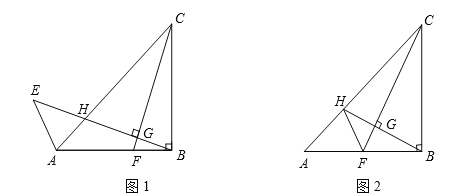
(1)如图1,延长GH到点E,使GE=GC,连接AE,求![]() 的度数;
的度数;
(2)如图2,若F为AB中点,连接FH,请探究BH、FH、CF的数量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将正面分别标有数字1、2、3的三张卡片洗匀后,背面朝上放在桌面上请完成下列各题
(1)随机抽取1张,求抽到卡片数字是奇数的概率;
(2)随机抽取一张作为十位上的数字(不放回),再抽取一张作为个位上的数字,能组成哪些两位数?
(3)在(2)的条件下,试求组成的两位数是偶数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ABD、∠ACD的角平分线交于点P,若∠A = 50°,∠D =10°,则∠P的度数为( )
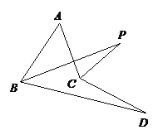
A.15°B.20°C.25°D.30°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五一节前夕,某商店从厂家购进![]() 两种礼盒,已知
两种礼盒,已知![]() 两种礼盒的单价比为
两种礼盒的单价比为![]() ,单价和为
,单价和为![]() 元
元
(1)求![]() 两种礼盒的单价分别是多少元?
两种礼盒的单价分别是多少元?
(2)该商店购进这两种礼盒恰好用去![]() 元,且购进
元,且购进![]() 种礼盒最多
种礼盒最多![]() 个,
个,![]() 种礼盒的数量不超过
种礼盒的数量不超过![]() 种礼盒数量的
种礼盒数量的![]() 倍,共有哪几种进货方案?
倍,共有哪几种进货方案?
(3)根据市场行情,销售一个![]() 种礼盒可获利
种礼盒可获利![]() 元,销售一个
元,销售一个![]() 种礼盒可获利
种礼盒可获利![]() 元.为奉献爱心,该商店决定每售出一个
元.为奉献爱心,该商店决定每售出一个![]() 种礼盒,为爱心公益基金捐款
种礼盒,为爱心公益基金捐款![]() 元,每个
元,每个![]() 种礼盒的利润不变,在(2)的条件下,要使礼盒全部售出后所有方案获利相同,
种礼盒的利润不变,在(2)的条件下,要使礼盒全部售出后所有方案获利相同,![]() 的值是多少?此时该商店可获利多少元?
的值是多少?此时该商店可获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在给定的一张平行四边形纸片上按如下操作:连结AC,作AC的垂直平分线MN分别交AD、AC、BC于M、O、N,连结AN,CM,则四边形ANCM是( )

A. 矩形 B. 菱形 C. 正方形 D. 无法判断
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com