
 如图,已知:OE、OF分别是AB、AC的垂直平分线,∠OBC、∠OCB的平分线交于点P,求证:OP⊥BC.
如图,已知:OE、OF分别是AB、AC的垂直平分线,∠OBC、∠OCB的平分线交于点P,求证:OP⊥BC.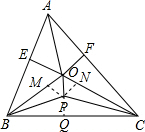 解:过点P作PM⊥OB于点M,作PN⊥OC于点N,作PQ⊥BC于点Q,
解:过点P作PM⊥OB于点M,作PN⊥OC于点N,作PQ⊥BC于点Q,

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
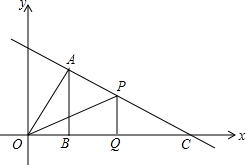 如图,一次函数y=-
如图,一次函数y=-| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
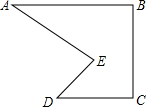 小明到工厂去进行社会实践活动,发现工人师傅生产了一种如图所示的零件,要求AB∥CD,∠BAE=30°.∠AED=70°.小明发现工人师傅只是量出∠BAE=30°.∠AED=70°后,又量了∠EDC=40°,就说AB与CD肯定是平行的,你知道是什么原因吗?
小明到工厂去进行社会实践活动,发现工人师傅生产了一种如图所示的零件,要求AB∥CD,∠BAE=30°.∠AED=70°.小明发现工人师傅只是量出∠BAE=30°.∠AED=70°后,又量了∠EDC=40°,就说AB与CD肯定是平行的,你知道是什么原因吗?查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,如果半径为1个单位长度的圆上有一点A,且点A与数轴上表示5.1的点重合(圆与数轴只有这一个交点),让圆沿数轴的负方向滚动一周,点A到达另一点B,则A,B两点之间表示整数的点共有( )
如图,如果半径为1个单位长度的圆上有一点A,且点A与数轴上表示5.1的点重合(圆与数轴只有这一个交点),让圆沿数轴的负方向滚动一周,点A到达另一点B,则A,B两点之间表示整数的点共有( )| A、5个 | B、6个 | C、7个 | D、8个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com