
【题目】如图,![]() 中,
中,![]() ,
,![]() 于点D,
于点D,![]() 交AC于点E,过点C在
交AC于点E,过点C在![]() 外部作
外部作![]() ,
,![]() 于点
于点![]() 连接EF.
连接EF.
![]() 求证:
求证:![]() ≌
≌![]() ;
;
![]() 判断四边形DCFE的形状,并说明理由.
判断四边形DCFE的形状,并说明理由.
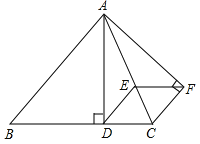
【答案】(1)证明详见解析;(2)四边形DCFE是菱形,理由详见解析.
【解析】
试题此题主要考查了全等三角形的判定与性质以及平行四边形和菱形的判定等知识,根据已知得出DE∥FC是解题关键.(1)首先利用平行线的性质得出∠FCE=∠BCA,进而利用全等三角形的判定方法AAS得出△AFC≌△ADC;(2)利用利用(1)中得结论易得出DE=FC,DE//FC,故四边形DCFE是平行四边形;再由DE=DC可判定四边形DCFE是菱形.
试题解析:
(1)证明:∵AB=BC,
∴∠BAC=∠BCA,
∵DE∥AB,CF∥AB,
∴DE∥FC,∠BAC=∠DEC,
∴∠DEC=∠BCA,∠DEC=∠FCE,
∴∠FCE=∠BCA,
在△AFC和△ADC中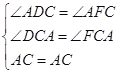 ,
,
∴△AFC≌△ADC(AAS);
四边形DCFE是菱形;理由如下:
∵∠DEC=∠BCA,DC=FC,
∴DE=DC,DE=FC,
又∵DE//FC,
∴四边形DCFE是平行四边形,
又∵DE=DC,
∴平行四边形DCFE是菱形.


科目:初中数学 来源: 题型:
【题目】甲班56人,其中身高在160厘米以上的男同学10人,身高在160厘米以上的女同学3人,乙班80人,其中身高在160厘米以上的男同学20人,身高在160厘米以上的女同学8人.如果想在两个班的160厘米以上的女生中抽出一个作为旗手,在哪个班成功的机会大?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
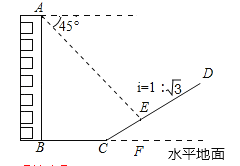
【题目】(8分)如图,一楼房AB后有一假山,其坡度为![]() ,山坡坡面上E点处有一休息亭,测的假山坡脚C与楼房水平距离BC=25米,与亭子距离CE=20米,小丽从楼房顶测得E点的俯角为45°,求楼房AB的高.(注:坡度i是指坡面的铅直高度与水平宽度的比)
,山坡坡面上E点处有一休息亭,测的假山坡脚C与楼房水平距离BC=25米,与亭子距离CE=20米,小丽从楼房顶测得E点的俯角为45°,求楼房AB的高.(注:坡度i是指坡面的铅直高度与水平宽度的比)
查看答案和解析>>
科目:初中数学 来源: 题型:
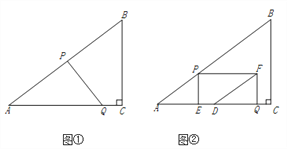
【题目】如图①,在Rt△ABC中,∠C=90°,AB=10,BC=6.点P从点A出发,沿折现AB—BC向终点C运动,在AB上以每秒5个单位长度的速度运动,在BC上以每秒3个单位长度的速度运动.点Q从点C出发,沿CA方向以每秒![]() 个单位长度的速度运动.点P、Q两点同时出发,当点P停止时,点Q也随之停止.设点P运动的时间为t秒.
个单位长度的速度运动.点P、Q两点同时出发,当点P停止时,点Q也随之停止.设点P运动的时间为t秒.
(1)求线段AQ的长.(用含t的代数式表示)
(2)当PQ与△ABC的一边平行时,求t的值
(3)如图②,过点P作PE⊥AC于点E,以PE、QE为邻边作矩形PEQF,点D为AC的中点,连结DF.直接写出DF将矩形PEQF分成两部分的面积比为1:2时t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
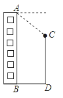
【题目】如图,小明在楼AB顶部的点A处测得楼前一棵树CD的顶端C的俯角为37°,已知楼AB高为18m,楼与树的水平距离BD为8.5m,则树CD的高约为________m(精确到0.1m).(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】袋子中装有3个带号码的球,球号分别是2,3,5,这些球除号码不同外其他均相同.
(1)从袋中随机摸出一个球,求恰好是3号球的概率;
(2)从袋中随机摸出一个球,再从剩下的球中随机摸出一个球,用树形图列出所有可能出现的结果,并求两次摸出球的号码之和为5的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
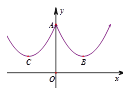
【题目】如图4所示的是桥梁的两条钢缆具有相同的抛物线形状.按照图中建立的直角坐标系,右面的一条抛物线的解析式为y=x2-4x+5表示,而且左右两条抛物线关于y轴对称,则左面钢缆的表达式为_________________________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com