
����Ŀ����������ѧ�����Żʱ������ʦ��ʾ���������⣺
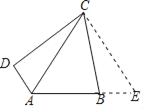
��ͼ������֪�ı���ABCD�У�ACƽ����DAB����DAB=120�㣬��B����D��������̽���߶�AB��AD��AC֮���������ϵ��
С������̽����������⣬����ʦ��ʾ��������ѧ�г�ͨ����һ���������⻯���ҵ�����˼·�������ǣ�С���룬�����ı���ABCD���⻯������ν�����⣺
��1�������������
��������������B=��D������ͼ����֪��Rt��CDA�У���DCA=30�㣬���ԣ�д����AD��AC֮���������ϵ��ͬ���ɵ�AB��AC��������ϵ���ɴ˵�AB��AD��AC֮���������ϵ��
��2�����ԭ������
�ܵ���1������������ԭ�����ϣ����Ӹ����ߣ�����C�ֱ���AB��AD�Ĵ��ߣ�����ֱ�ΪE��F����ͼ������д��̽�����̣�
��3�����˼
��һ���⡱����ѧ���������֮һ��С��������ʦ�������£���̽�����۵����������ͼ�е�60��ǣ�ͨ������ȱ������Σ�����������ȫ��ͬ������˸����⣬����ͼ�������������ߣ����������̽�����̣�

���𰸡���1��AD=![]() AC��AD+AB=AC����2��AB+AD=AC��̽�����̼���������3��AC= AB+AD��̽�����̼�����.
AC��AD+AB=AC����2��AB+AD=AC��̽�����̼���������3��AC= AB+AD��̽�����̼�����.
��������
��1�����ݡ�B+��D=180���ҡ�B=��D֪��B=��D=90������ACƽ�֡�DAB����DAB=120��֪��DAC=��BAC=60��������ֱ��������30��������ֱ�DZߵ���б�ߵ�һ�����ɵã�
��2����֤��CDF�ա�CBE��DF=BE���ݴ˵�AB+AD=AE+BE+AD=AE+DF+AD=AE+AF=AC��
��3���ӳ�AB����E��ʹ��AE=AC���ݴ˿ɵ���ACEΪ�ȱ������Σ���һ��֪AC=EC����DAC=��E=60����֤��ADC�ա�EBC��AD=EB����һ�����ɵã�
��1���ߡ�B+��D=180�����ҡ�B=��D��
���B=��D=90�㣬
�֡�ACƽ�֡�DAB����DAB=120�㣬
���DAC=��BAC=60�㣬
���ACD=��ACB=30�㣬
��AD=![]() AC��AB=
AC��AB=![]() AC��
AC��
��AD+AB=![]() AC+
AC+![]() AC=AC��
AC=AC��
��2����ACΪ��DAB��ƽ���ߣ�CF��AD��CE��AB��
��CF=CE��
�ߡ�B���ADC��������ADC���CDF������
���CDF=��B��
�֡ߡ�F=��CEB=90�㣬
���CDF�ա�CBE��AAS����
��DF=BE��
��AB+AD
=AE+BE+AD
=AE+DF+AD
=AE+AF
=AC��
��AB+AD=AC��
��3����ͼ���ӳ�AB����E��ʹ��AE=AC��
�ߡ�CAB=![]() ��BAD=60�㣬
��BAD=60�㣬
���ACEΪ�ȱ������Σ�
��AC=EC����DAC=��E=60�㣮
�֡ߡ�ABC���D������
���D=��CBE��
���ADC�ա�EBC��AAS����
��AD=EB��
��AC=AE=AB+EB=AB+AD��


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
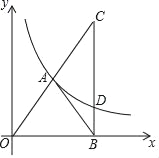
����Ŀ����֪����ͼ������������y=![]() ��ͼ���ϵ�һ��A��m��n���ڵ�һ�����ڣ���B��x����������ϣ���AB=AO������B��BC��x�ᣬ���߶�OA���ӳ����ཻ�ڵ�C���뷴����������ͼ���ཻ�ڵ�D��
��ͼ���ϵ�һ��A��m��n���ڵ�һ�����ڣ���B��x����������ϣ���AB=AO������B��BC��x�ᣬ���߶�OA���ӳ����ཻ�ڵ�C���뷴����������ͼ���ཻ�ڵ�D��
��1���ú�m�Ĵ���ʽ��ʾ��D�����ꣻ
��2����֤��CD=3BD��
��3������AD��OD��������ABD���������AOD������ı�ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y=��2x��ͼ������κ���y=��x2+3xͼ��ĶԳ��ύ�ڵ�B��
��1�����B��������
��2����֪��P�Ƕ��κ���y=��x2+3xͼ����y���Ҳಿ���ϵ�һ�����㣬��ֱ��y=��2x��y������ƽ�ƣ��ֱ�x�ᡢy����C��D���㣮����CDΪֱ�DZߵġ�PCD���OCD���ƣ����P������Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽�ij�о��꼶ѧ��ѧҵ���������ɼ����ִ��������ȡ����ѧ���������ɼ����зֶ�ͳ�����£�
ѧҵ���������ɼ��������Σ�ͳ�Ʊ� | ||
������ | �������ˣ� | Ƶ�� |
A | 48 | 0.2 |
B | a | 0.25 |
C | 84 | 0.35 |
D | 36 | b |
E | 12 | 0.05 |
������Ϊ����A��50�֣�B��49��45�֣�C��44��40�֣�D��39��30�֣�E��29��0�֣� 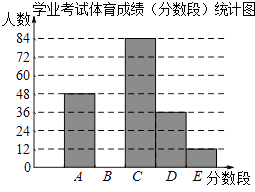
���������ṩ����Ϣ���ش��������⣺
��1����ͳ�Ʊ��У�a��ֵΪ �� b��ֵΪ ��
��2����ͳ��ͼ������������ܰ��ʾ����ͼʱ��������0.5�������ϵĺ�ɫǩ�ֱ�Ϳ�ڣ���
��3����ͬѧ˵�����ҵ������ɼ��Ǵ˴γ��������������ݵ���λ���������ʣ���ͬѧ�������ɼ�Ӧ��ʲô�������ڣ�������Ӧ�����ε���ĸ��
��4������ѳɼ���40�����ϣ���40�֣���Ϊ���㣬��ô���н���10440�����꼶ѧ���������ɼ�Ϊ�����ѧ������Լ�ж�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������8�֣���ͼ���������ABCDE�У���BCD=��EDC=90����BC=ED��AC=AD��
��1����֤����ABC�ա�AED��
��2������B=140��ʱ������BAE�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУΪ�˽���꼶ѧ��������״�����Ӱ��꼶ѧ���������ȡ����ѧ�����а˰��������ܲ��ԣ����Խ����ΪA��B��C��D�ĸ��ȼ������������ͳ��ͼ�е���Ϣ�ش��������⣺
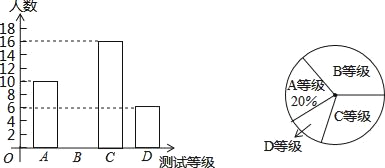
��1���β��Թ������˶�����ѧ����
��2���β��Խ��ΪB�ȼ���ѧ����������ȫ����ͳ��ͼ��
��3�������������ͳ��ͼ�а��꼶ѧ�����ܲ��Խ��ΪD�ȼ�������Բ�ĽǵĶ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����E��50�㣬��BAC��50�㣬��D��110�������ABD�Ķ�����
�����ƽ����̣�������������д��Ӧ���������ݣ�
�⣺�ߡ�E��50�㣬��BAC��50��������֪��
���E���� ��������������
���� ������ �������� ����
���ABD+��D��180�㣮���� ����
���D��110��������֪��
���ABD��70��������ʽ�����ʣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��ֱ������CD��AB�ڵ�E������B����O�����ߣ���AC���ӳ����ڵ�F����֪OA=3��AE=2�� 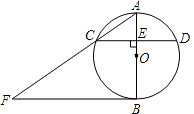
��1����CD�ij���
��2����BF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����OΪֱ��AB��һ�㣬��һֱ�����ǰ�OMN��ֱ�Ƕ�����ڵ�O��������OCƽ�֡�MOB��
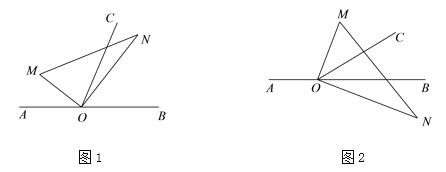
(1)��ͼ1������AOM=30�㣬���CON�Ķ�����
(2)��ͼ1�У�����AOM=a��ֱ��д����CON�Ķ������ú�a�Ĵ���ʽ��ʾ����
(3)��ͼ1�е�ֱ�����ǰ�OMN�ƶ���O˳ʱ����ת��ͼ2��λ�ã�һ��OM������OB�Ϸ�����һ��ON��ֱ��AB���·���
��̽����AOM�͡�CON�Ķ���֮��Ĺ�ϵ��д����Ľ��ۣ���˵�����ɣ�
�ڵ���AOC=3��BONʱ�����AOM�Ķ�����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com