
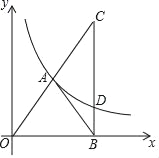
【题目】已知:如图,反比例函数y=![]() 的图象上的一点A(m,n)在第一象限内,点B在x轴的正半轴上,且AB=AO,过点B作BC⊥x轴,与线段OA的延长线相交于点C,与反比例函数的图象相交于点D.
的图象上的一点A(m,n)在第一象限内,点B在x轴的正半轴上,且AB=AO,过点B作BC⊥x轴,与线段OA的延长线相交于点C,与反比例函数的图象相交于点D.
(1)用含m的代数式表示点D的坐标;
(2)求证:CD=3BD;
(3)联结AD、OD,试求△ABD的面积与△AOD的面积的比值.
【答案】(1)D(2m,![]() );(2)详见解析;(3)
);(2)详见解析;(3)![]() .
.
【解析】
(1)先用m表示点A的坐标,进而利用等腰三角形的性质得出点B的坐标,即可得出结论;
(2)先确定出直线OA的解析式,即可得出点C的坐标,求出CD,BD即可得出结论;
(3)先判断出S△ACD=3S△ABD,再判断出S△AOD=S△ACD,即可得出结论.
(1)如图,
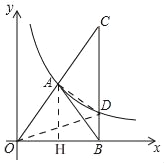
∵点A(m,n)在反比例函数y=![]() 的图象上,
的图象上,
∴n=![]() ,
,
∴A(m,![]() ),
),
过点A作AH⊥x轴于H,
∴H(m,0),
∵AB=OA,
∴OB=2OH,
∴B(2m,0),
∵BD⊥x轴于D,
∴点D的横坐标为2m,
∵点D在反比例函数y=![]() 的图象上,
的图象上,
∴D(2m,![]() );
);
(2)设直线AO的解析式为y=kx,
∵点A(m,![]() ),
),
∴![]() ,
,
∴k=![]() ,
,
∴直线AO的解析式为y=![]() x,
x,
∵点C在直线AO上,且横坐标为2m,
∴C(2m,![]() ),
),
∴CD=![]() ,
,
∵BD=![]() ,
,
∴CD=3BD;
(3)由(2)知,CD=3BD,
∴S△ACD=3S△ABD,
∵AB=AO,
∴∠AOB=∠ABO,
∵∠CBO=90°,
∴∠AOB+∠C=90°,∠ABO+∠ABC=90°,
∴∠C=∠ABC,
∴AB=AC,
∴AC=AO,
∴S△AOD=S△ACD,
∴S△AOD=3S△ABD,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】新华书店推出售书优惠方案:一次性购书不超过100 元,不享受优惠;一次性购书超过100元但不超过200元一律打九折;一次性购书200元以上一律打八折.
(1)如果小明一次性购书的原价为250元,那么他实际付款_________元;
(2)如果小华同学一次性购书付款162元,那么小华所购书的原价为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知有理数a,b,c在数轴上所对应的点分别是A,B.C三点,且a,b满足,①多项式![]() x|a|+(a﹣2)x+7是关于x的二次三项式:②(b﹣1)2+|c﹣5|=0
x|a|+(a﹣2)x+7是关于x的二次三项式:②(b﹣1)2+|c﹣5|=0
(1)请在图1的数轴上描出A,B,C三点,并直接写出a,b,c三数之间的大小关系 用“<”连接);
(2)点P为数轴上C点右侧一点,且点P到A点的距离是到C点距高的2倍,求点P在数轴上所对应的有理数;
(3)点A在数轴上以每秒1个单位长度的速度向左运动,同时点B和点C在数轴上分别以每秒m个单位长度和4个单位长度的速度向右运动(其中m<4),若在整个运动的过程中,点B到点A的距离与点B到点C的距离差始终不变,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市开展了“雷锋精神你我传承,关爱老人从我做起”的主题活动,随机调查了本市部分老人与子女同住情况,根据收集到的数据,绘制成如下统计图表(不完整) 老人与子女同住情况百分比统计表
老人与子女 | 同住 | 不同住 | 不同住 | 其他 |
A | 50% | B | 5% |
根据统计图表中的信息,解答下列问题: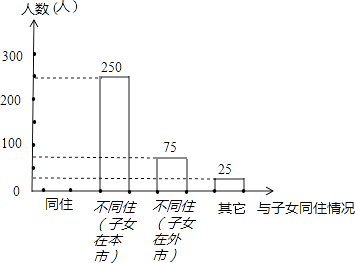
(1)求本次调查的老人的总数及a、b的值;
(2)将条形统计图补充完整;(画在答卷相对应的图上)
(3)若该市共有老人约15万人,请估计该市与子女“同住”的老人总数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业研制的产品今年第一季度的销售数量为300件,第二季度由于市场等因素,销售数量比第一季度减少了4%,从第三季度起,该企业搞了一系列的促销活动,销售数量又有所提升,第四季度的销售量达到了450件,假设第三季度与第四季度销售数量的增长率相同,求这个增长率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=k(x+1)(x﹣ ![]() )与x轴交于点A,B,与y轴交于点C,则能使△ABC为等腰三角形的抛物线的条数是( )
)与x轴交于点A,B,与y轴交于点C,则能使△ABC为等腰三角形的抛物线的条数是( )
A.2
B.3
C.4
D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)某市在道路改造过程中,需要铺设一条长为1000米的管道,决定由甲、乙两个工程队来完成这一工程.已知甲工程队比乙工程队每天能多铺设20米,且甲工程队铺设350米所用的天数与乙工程队铺设250米所用的天数相同.
(1)甲、乙工程队每天各能铺设多少米?
(2)如果要求完成该项工程的工期不超过10天,那么为两工程队分配工程量(以百米为单位)的方案有几种?请你帮助设计出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一个边长为a的大正方形,剪去一个边长为b的小正方形,即图①称之为“前世”,然后再剪拼成一个新长方形如图②称之为“今生”,请你解答下面的问题:

(1)“前世”图①的面积与“今生”图②新长方形的面积 ;
(2)根据图形面积的和差关系直接写出“前世”图①的面积为: ,标明“今生”图②新长方形的长为 、宽为 ,面积为: .
(3)“形缺数时少直观,数缺形式少形象”它体现了数学的数形结合思想,由(1)和(2)图形面积的计算,形象的验证了代数中的一个乘法公式为: .
(4)请你根据(3)题中乘法公式,计算:2.001×1.999.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“魅力数学”社团活动时,张老师出示了如下问题:
如图①,已知四边形ABCD中,AC平分∠DAB,∠DAB=120°,∠B与∠D互补,试探究线段AB,AD,AC之间的数量关系;
小敏反复探索,不得其解,张老师提示道:“数学中常通过把一个问题特殊化来找到解题思路”,于是,小敏想,若将四边形ABCD特殊化,看如何解决问题:
(1)特殊情况入手
添加条件:“∠B=∠D”,如图②易知在Rt△CDA中,∠DCA=30°,所以,写出边AD与AC之间的数量关系,同理可得AB与AC的数量关系,由此得AB,AD,AC之间的数量关系;
(2)解决原来问题
受到(1)的启发,在原问题上,添加辅助线,过点C分别作AB,AD的垂线,垂足分别为E、F,如图③,请写出探究过程;
(3)解后反思
“一题多解”是数学解题的魅力之一,小敏在张老师的引导下,受探究结论的启发,结合图中的60°角,通过构造等边三角形,利用三角形全等同样解决了该问题,请在图①中作出辅助线,并简述你的探究过程.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com