
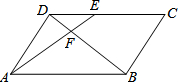
 如图,在平行四边形ABCD中,E为CD上一点,连接AE、BD,且AE、BD交于点F,S△DEF:S△ABF=4:25,则S△ADF:S四边形BCEF为( )
如图,在平行四边形ABCD中,E为CD上一点,连接AE、BD,且AE、BD交于点F,S△DEF:S△ABF=4:25,则S△ADF:S四边形BCEF为( )| A. | 10:31 | B. | 10:21 | C. | 4:25 | D. | 4:21 |
分析 先证明△DEF∽△BAF,得出$\frac{DE}{AB}$=$\frac{EF}{AF}$=$\frac{2}{5}$,得出$\frac{{S}_{△DEF}}{{S}_{△ADF}}$=$\frac{EF}{AF}$=$\frac{2}{5}$=$\frac{4}{10}$,再得出$\frac{{S}_{△ADF}}{{S}_{△ABD}}$=$\frac{10}{35}$,即可得出结果.
解答 解:∵四边形ABCD是平行四边形,
∴AB=DC,DC∥AB,S△BCD=S△ABD,
∴△DEF∽△BAF,
∴$\frac{{S}_{△DEF}}{{S}_{△BAF}}$=$(\frac{DE}{AB})^{2}$=$\frac{4}{25}$,
∴$\frac{DE}{AB}$=$\frac{EF}{AF}$=$\frac{2}{5}$,
∴$\frac{{S}_{△DEF}}{{S}_{△ADF}}$=$\frac{EF}{AF}$=$\frac{2}{5}$=$\frac{4}{10}$,
∴$\frac{{S}_{△ADF}}{{S}_{△ABD}}$=$\frac{10}{10+25}$=$\frac{10}{35}$,
∴$\frac{{S}_{△ADF}}{{S}_{四边形BCEF}}$=$\frac{10}{35-4}$=$\frac{10}{31}$;
故选:A.
点评 本题考查了平行四边形的性质、相似三角形的判定与性质以及面积的计算方法;熟练掌握平行四边形的性质,证明三角形相似是解决问题的关键.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源:2016-2017学年江苏省南通市七年级3月月考数学试卷(解析版) 题型:单选题
如果m=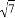 -1,那么m的取值范围是( ).
-1,那么m的取值范围是( ).
A. 0<m<1 B. 1<m<2 C. 2<m<3 D. 3<m<4
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
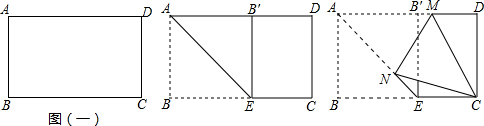
| A. | 6-2$\sqrt{3}$ | B. | 3$\sqrt{2}$-6 | C. | 6$\sqrt{3}$-6 | D. | $\sqrt{3}$+$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com