
【题目】已知,在Rt![]() 中,
中,![]() ,点
,点![]() 是斜边
是斜边![]() 的中点,
的中点,![]() ,且
,且![]() ,
,![]() 于点
于点![]() ,联结
,联结![]() .
.
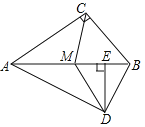
(1)求证:![]()
![]()
![]() ;
;
(2)当![]() 时,求
时,求![]() 的值;
的值;
(3)在(2)的条件下,求![]() 的值.
的值.
【答案】(1)见解析;(2)S△BED:S△MED=1:3;(3)cos∠ABC=![]() .
.
【解析】
(1)易证∠DME=∠CBA,∠ACB=∠MED=90°,从而可证明△MED∽△BCA;
(2)由∠ACB=90°,点M是斜边AB的中点,可知MB=MC=AM,从而可证明MD=CM=MB=![]() AB,从而证得S△AMC=S△BNC=
AB,从而证得S△AMC=S△BNC=![]() S△ABC,由S△BDM=
S△ABC,由S△BDM=![]() 证得
证得![]() ,从而证得S△BED:S△MED=1:3;
,从而证得S△BED:S△MED=1:3;
(3)由![]() ,得到
,得到![]() ,进一步得到
,进一步得到![]() ,证得cos∠EMD=
,证得cos∠EMD=![]() ,由∠DME=∠CBA,证得cos∠ABC=
,由∠DME=∠CBA,证得cos∠ABC=![]() .
.
解:(1)∵MD∥BC,
∴∠DME=∠CBA,
∵∠ACB=∠MED=90°,
∴△MED∽△BCA,
(2)∵∠ACB=90°,点M是斜边AB的中点,
∴MB=MC=AM=![]() AB,
AB,
∵MC=MD,
∴MD=![]() AB,
AB,
∴S△AMC=S△BNC=![]() S△ABC,
S△ABC,
∵△MED∽△BCA,
∴![]() =(
=(![]() )2=
)2=![]() ,
,
∵S△BDM=![]() ,
,
∴![]() ,
,
∴S△BED:S△MED=1:3;
(3)∵![]() ,
,
∴![]() ,
,
∵MD=MB,
∴![]() ,
,
∴cos∠EMD=![]() ,
,
∵∠DME=∠CBA,
∴cos∠ABC=![]() .
.


科目:初中数学 来源: 题型:
【题目】已知:平行四边形![]() ,对角线
,对角线![]() 点P为射线BC上一点,
点P为射线BC上一点,![]() ,(点M与点B分别在直线AP的两侧),且
,(点M与点B分别在直线AP的两侧),且![]() 联结MD.
联结MD.
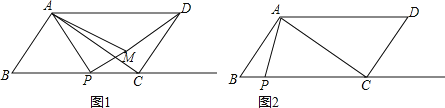
(1)当点M在![]() 内时,如图一,设
内时,如图一,设![]() 求
求![]() 关于
关于![]() 的函数解析式.
的函数解析式.
(2)请在图二中画出符合题意得示意图,并探究:图中是否存在与![]() 相似的三角形?若存在,请写出证明过程,若不存在,请说明理由
相似的三角形?若存在,请写出证明过程,若不存在,请说明理由
(3)当![]() 为等腰三角形时,求
为等腰三角形时,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() (
(![]() >0)与一次函数
>0)与一次函数![]() 的图像交于B,C两点,一次函数
的图像交于B,C两点,一次函数![]() 图像与y轴交于点A.
图像与y轴交于点A.


(1)当k=3,a+b=4时,
①求B,C两点的坐标;
②求△OBC的面积![]() ;
;
(2)当k=1时,设B、C两点坐标为 B(a,b)(a≥2)、C(c,d)(点B、C不重合).
①求ac的值;
②设△OAC面积为![]() ,求
,求![]() 与b的函数关系式,并直接写出
与b的函数关系式,并直接写出![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着生活水平的不断提高,越来越多的人选择到电影院观看电影,体验视觉盛宴,并且更多的人通过网上平台购票,既快捷又能享受更多优惠.某电影城2019年从网上购买![]() 张电影票的费用比现场购买
张电影票的费用比现场购买![]() 张电影票的费用少
张电影票的费用少![]() 元:从网上购买
元:从网上购买![]() 张电影票的费用和现场购买
张电影票的费用和现场购买![]() 张电影票的费用共
张电影票的费用共![]() 元.
元.
(1)求该电影城2019年在网上购票和现场购票每张电影票的价格为多少元?
(2)2019年五一当天,该电影城按照2019年网上购票和现场购票的价格销售电影票,当天售出的总票数为![]() 张.五一假期过后,观影人数出现下降,于是电影城决定从5月5日开始调整票价:现场购票价格下调,网上购票价格不变,结果发现,现场购票每张电影票的价格每降低
张.五一假期过后,观影人数出现下降,于是电影城决定从5月5日开始调整票价:现场购票价格下调,网上购票价格不变,结果发现,现场购票每张电影票的价格每降低![]() 元,售出总票数就比五一当天增加
元,售出总票数就比五一当天增加![]() 张.经统计,5月5日售出的总票数中有
张.经统计,5月5日售出的总票数中有![]() 的电影票通过网上售出,其余通过现场售出,且当天票房总收入为
的电影票通过网上售出,其余通过现场售出,且当天票房总收入为![]() 元,试求出5月5日当天现场购票每张电影票的价格为多少元?
元,试求出5月5日当天现场购票每张电影票的价格为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一元二次方程中,有著名的韦达定理:对于一元二次方程ax2+bx+c=0(a≠0),如果方程有两个实数根x1,x2,那么x1+x2=![]() ,x1+x2=
,x1+x2=![]() (说明:定理成立的条件△≥0).比如方程2x2-3x-1=0中,△=17,所以该方程有两个不等的实数解.记方程的两根为x1,x2,那么x1+x2=
(说明:定理成立的条件△≥0).比如方程2x2-3x-1=0中,△=17,所以该方程有两个不等的实数解.记方程的两根为x1,x2,那么x1+x2=![]() ,x1+x2=
,x1+x2=![]() .请阅读材料回答问题:
.请阅读材料回答问题:
(1)已知方程x2-3x-2=0的两根为x1、x2,求下列各式的值:
①x12+x22;②![]() ;
;
(2)已知x1,x2是一元二次方程4kx2-4kx+k+1=0的两个实数根.
①是否存在实数k,使(2x1-x2)(x1-2x2)=![]() 成立?若存在,求出k的值;若不存在,请说明理由;
成立?若存在,求出k的值;若不存在,请说明理由;
②求使![]() -2的值为整数的实数k的整数值.
-2的值为整数的实数k的整数值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年中秋节来期间,某超市以每盒80元的价格购进了1000盒月饼,第一周以每盒168元的价格销售了300盒,第二周如果单价不变,预计仍可售出300盒,该超市经理为了增加销量,决定降价,据调查,单价每降低1元,可多售出10盒,但最低每盒要赢利30元,第二周结束后,该超市将对剩余的月饼一次性赔钱甩卖,此时价格为70元/盒.
(1)若设第二周单价降低x元,则第二周的单价是 ______ ,销量是 ______ ;
(2)经两周后还剩余月饼 ______ 盒;
(3)若该超市想通过销售这批月饼获利51360元,那么第二周的单价应是多元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为积极参与鄂州市全国文明城市创建活动,我市某校在教学楼顶部新建了一块大型宣传牌,如下图.小明同学为测量宣传牌的高度![]() ,他站在距离教学楼底部
,他站在距离教学楼底部![]() 处6米远的地面
处6米远的地面![]() 处,测得宣传牌的底部
处,测得宣传牌的底部![]() 的仰角为
的仰角为![]() ,同时测得教学楼窗户
,同时测得教学楼窗户![]() 处的仰角为
处的仰角为![]() (
(![]() 、
、![]() 、
、![]() 、
、![]() 在同一直线上).然后,小明沿坡度
在同一直线上).然后,小明沿坡度![]() 的斜坡从
的斜坡从![]() 走到
走到![]() 处,此时
处,此时![]() 正好与地面
正好与地面![]() 平行.
平行.
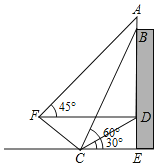
(1)求点![]() 到直线
到直线![]() 的距离(结果保留根号);
的距离(结果保留根号);
(2)若小明在![]() 处又测得宣传牌顶部
处又测得宣传牌顶部![]() 的仰角为
的仰角为![]() ,求宣传牌的高度
,求宣传牌的高度![]() (结果精确到0.1米,
(结果精确到0.1米,![]() ,
,![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在⊙O中,直径AB=6,BC是弦,∠ABC=30°,点P在BC上,点Q在⊙O上,且OP⊥PQ.
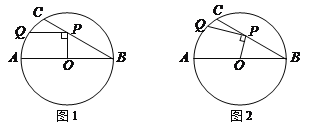
(1)如图1,当PQ∥AB时,求PQ的长度;
(2)如图2,当点P在BC上移动时,求PQ长的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com