
【题目】已知:平行四边形![]() ,对角线
,对角线![]() 点P为射线BC上一点,
点P为射线BC上一点,![]() ,(点M与点B分别在直线AP的两侧),且
,(点M与点B分别在直线AP的两侧),且![]() 联结MD.
联结MD.
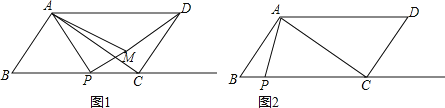
(1)当点M在![]() 内时,如图一,设
内时,如图一,设![]() 求
求![]() 关于
关于![]() 的函数解析式.
的函数解析式.
(2)请在图二中画出符合题意得示意图,并探究:图中是否存在与![]() 相似的三角形?若存在,请写出证明过程,若不存在,请说明理由
相似的三角形?若存在,请写出证明过程,若不存在,请说明理由
(3)当![]() 为等腰三角形时,求
为等腰三角形时,求![]() 的长.
的长.
【答案】(1) ;(2)
;(2)![]() ,证明见解析;(3)7.5或3或27.
,证明见解析;(3)7.5或3或27.
【解析】
(1)作AE⊥BC于E,先在Rt△ABC中运用勾股定理求出BC=15,再解Rt△ABE,得到AE=![]() ,BE=
,BE=![]() ,然后在Rt△AEP中,利用勾股定理得AP2=PE2+AE2,即可求出y关于x的函数关系式;
,然后在Rt△AEP中,利用勾股定理得AP2=PE2+AE2,即可求出y关于x的函数关系式;
(2)先由两角对应相等的两三角形相似证明出△APM∽△ACD,则AP:AC=AM:AD,即AP:AM=AC:AD,又由∠PAM=∠CAD,得出∠PAC=∠MAD,根据两边对应成比例且夹角相等的两三角形相似即可得到△PAC∽△MAD;
(3)先由相似三角形的形状相同,由(2)得出△APC为等腰三角形,再分两种情况进行讨论:①点M在平行四边形内;②点M在平行四边形外;又分两种情况:(i)P在BC上,(ii)P在BC的延长线上.
解:(1)如图,作AE⊥BC于E,
在Rt△ABC中,∵AB=9,AC=12,
∴BC=15,
∵△ABE∽△CBA,
∴BE=![]() ,AE=
,AE=![]()
∵BP=![]() ,∴PE=
,∴PE=![]() ,
,
在Rt△AEP中,![]()
∴
(2) 存在,![]() ,
,
∵∠PAM=∠CAD,∠APM=∠ACD=90°,
∴△APM∽△ACD,
∴![]()
∴![]()
∵![]() ,
,
∴∠PAC=∠MAD,
∴![]()
(3)∵△PAC∽△MAD,
∴当△AMD为等腰三角形时,△APC也为等腰三角形,
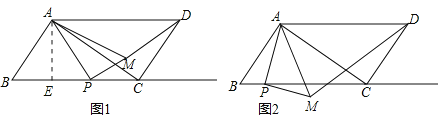
①当点M在平行四边形内时,如图1.点P只能在EC上,
∵∠APC为钝角,
∴∠PAC=∠PCA,
∴PC=PA,
又∵∠PAB=90°-∠PAC,∠B=90°-∠PCA,
∴∠PAB=∠B,∴PA=PB,
∴PA=PB=PC=![]() BC=
BC=![]() ,
,
即BP=7.5;
②当点M在平行四边形外时,
(i)若P在BC上,如图2.点P只能在BE上,
∵AP<AC,AP<PC,
∴CA=CP=12,则BP=15-12=3;
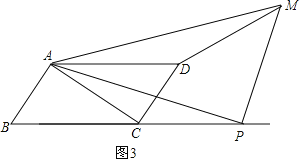
(ii)若P在BC的延长线上,如图3,
∵AP>AC,AP>PC,
∴CA=CP=12,则BP=15+12=27.
综上可知,当△AMD为等腰三角形时,BP的长为7.5或3或27.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 与x轴交于A、B两点,与y轴交于C点,B点与C点是直线y=x﹣3与x轴、y轴的交点.D为线段AB上一点.
与x轴交于A、B两点,与y轴交于C点,B点与C点是直线y=x﹣3与x轴、y轴的交点.D为线段AB上一点.

(1)求抛物线的解析式及A点坐标.
(2)若点D在线段OB上,过D点作x轴的垂线与抛物线交于点E,求出点E到直线BC的距离的最大值.
(3)D为线段AB上一点,连接CD,作点B关于CD的对称点B′,连接AB′、B′D
①当点B′落坐标轴上时,求点D的坐标.
②在点D的运动过程中,△AB′D的内角能否等于45°,若能,求此时点B′的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
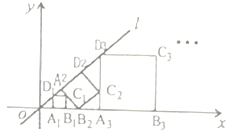
【题目】如图,在平面直角坐标系中,直线![]() 为正比例函数
为正比例函数![]() 的图象,点
的图象,点![]() 的坐标为
的坐标为![]() ,过点
,过点![]() 作
作![]() 轴的垂线交直线
轴的垂线交直线![]() 于点
于点![]() ,以
,以![]() 为边作正方形
为边作正方形![]() ;过点
;过点![]() 作直线
作直线![]() 的垂线,垂足为
的垂线,垂足为![]() ,交
,交![]() 轴于点
轴于点![]() ,以
,以![]() 为边作正方形
为边作正方形![]() ;过点
;过点![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,交直线
,交直线![]() 于点
于点![]() ,以
,以![]() 为边作正方形
为边作正方形![]() ,…,按此规律操作下所得到的正方形
,…,按此规律操作下所得到的正方形![]() 的面积是
的面积是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
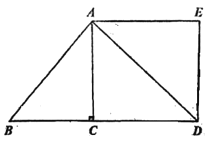
【题目】如图,在Rt![]() 中,∠ACB=90°,
中,∠ACB=90°,![]() ,AC=4;D是BC的延长线上一个动点,∠EDA=∠B,AE//BC.
,AC=4;D是BC的延长线上一个动点,∠EDA=∠B,AE//BC.
(1)找出图中的相似三角形,并加以证明;
(2)设![]() ,
,![]() ,求
,求![]() 关于
关于![]() 的函数解析式,并写出函数的定义域;
的函数解析式,并写出函数的定义域;
(3)当![]() 为等腰三角形时,求AE的长.
为等腰三角形时,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】蜂蜜具有消食、润肺、安神、美颜之功效,是天然的健康保健佳品.秋天即将来临时,雪宝山土特产公司抓住商机购进甲、乙、丙三种蜂蜜,已知销售每瓶甲蜂蜜的利润率为10%,每瓶乙蜂蜜的利润率为20%,每瓶丙蜂蜜的利润率为30%.当售出的甲、乙、丙蜂蜜瓶数之比为1:3:1时,商人得到的总利润率为22%;当售出的甲、乙、丙蜂蜜瓶数之比为3:2:1时,商人得到的总利润率为20%.那么当售出的甲、乙、丙蜂蜜瓶数之比为5:6:1时,该公司得到的总利润率为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
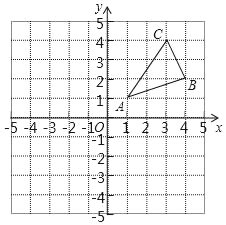
【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1)请画出△ABC向左平移5个单位长度后得到的△A1B1C1;
(2)请画出△ABC关于原点对称的△A2B2C2;并写出点A2、B2、C2坐标;
(3)请画出△ABC绕O逆时针旋转90°后的△A3B3C3;并写出点A3、B3、C3坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com